Pravděpodobnostní funkce

Pravděpodobnostní funkce poctivé kostky. U všech čísel na kostce je stejná pravděpodobnost, že se při hodu objeví na horní stěně.

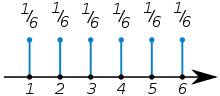
Předpokládejme, že X: Ω → A (${\displaystyle \subseteq \mathbb {R} }$) je diskrétní náhodná veličina definovaná na prostoru elementárních jevů Ω. Pak pravděpodobnostní funkce f_X: A → <0, 1> pro X je definovaná jako[3][4]

${\displaystyle f_{X}(x)=\Pr(X=x)=\Pr(\{\omega \in \Omega :X(\omega )=x\}).}$

Abychom se vyhnuli chybám, můžeme uvažovat o pravděpodobnosti jako o hmotě, protože fyzická hmota je zachována stejně jako celková pravděpodobnost pro všechny hypotetické výsledky x:

${\displaystyle \sum _{x\in A}f_{X}(x)=1}$

Když existuje přirozené pořadí mezi hypotézami x, může být pohodlné jim přiřadit numerické hodnoty (nebo n-ticím v případě diskrétní vícerozměrné náhodné veličiny) a uvažovat také hodnoty, které nejsou v obrazu množiny X. To znamená, že funkce f_X může být definovaná pro všechna reálná čísla a f_X(x) = 0 pro všechna x ${\displaystyle \notin }$ X(Ω), jak je znázorněno na obrázku.

Protože obraz X je spočetný, pravděpodobnostní funkce f_X(x) je nulová pro všechny hodnoty s výjimkou spočetného počtu hodnot x. Nespojitost pravděpodobnostní funkce plyne z faktu, že distribuční funkce diskrétní náhodné veličiny je také nespojitá. Pokud je derivovatelná, její derivace je nula, stejně jako pravděpodobnostní funkce je nulová ve všech takových bodech.

Předpokládejme, že Ω je prostor elementárních jevů všech výsledků jediného hodu mincí a X je náhodná veličina definovaná na Ω přiřazením 0 „orlu“ a 1 „hlavě“; jedná se o alternativní rozdělení, které je speciálním případem binomického rozdělení pro počet hodů n=1. Pokud je mince poctivá, pravděpodobnostní funkce je

${\displaystyle f_{X}(x)={\begin{cases}{\frac {1}{2}},&x\in \{0,1\},\\0,&x\notin \{0,1\}.\end{cases}}}$

Příkladem vícerozměrného diskrétního rozdělení a jeho pravděpodobnostní funkce je multinomické rozdělení.