Oddělovací axiom
Oddělovací axiomy jsou různé podmínky, které v topologii a příbuzných oborech matematiky klademe na topologické prostory, abychom zajistili, že prostory budou mít určité vlastnosti (budou určitého druhu). Tyto podmínky se někdy nazývají Tichonovovy oddělovací axiomy podle Andreje Nikolajeviče Tichonova.
| Oddělovací axiomy v topologických prostorech | |
|---|---|
| Kolmogorovova klasifikace | |
| T0 | (Kolmogorovův) |
| T1 | (Fréchetův) |
| T2 | (Hausdorffův) |
| T2,5 | (Urysohnův) |
| úplně T2 | (úplně Hausdorffův) |
| T3 | (regulární Hausdorffův) |
| T3,5 | (Tichonovův) |
| T4 | (normální Hausdorffův) |
| T5 | (úplně normální Hausdorffův) |
| T6 | (perfektně normální Hausdorffův) |
| |
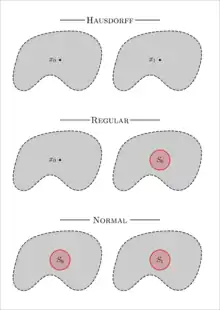
Oddělovací axiomy ve skutečnosti nejsou axiomy v obvyklém smyslu. Mají ten význam, že na topologický prostor můžeme klást další podmínky, abychom získali speciální vlastnosti topologického prostoru. Moderní přístup je provést axiomatizaci topologického prostoru jednou provždy, a pak uvažovat o různých druzích topologických prostorů. Termín „oddělovací axiom“ se však udržel; vychází z něho i označování oddělovacích axiomů písmenem „T“ z německého Trennungsaxiom, což znamená „oddělovací axiom“.
Přesné významy jednotlivých oddělovacích axiomů se během času měnily, jak je vysvětleno v článku Historie separačních axiomů. Při čtení starší literatury je důležité vědět, co přesně znamenají jednotlivé podmínky, aby bylo jasné, o jakém typu topologických prostorů autor mluví.
Předběžné definice
Než definujeme samotné oddělovací axiomy, uvedeme konkrétní význam konceptu oddělených množin (a bodů) v topologických prostorech. (Oddělené množiny nejsou totéž jako oddělené prostory definované v další části.)
Oddělovací axiomy jsou topologickým nástrojem pro rozlišování disjunktních množin a různých bodů. Pro prvky topologického prostoru nestačí, aby byly různé (tj. neidentické); chceme, aby byly topologicky rozlišitelné. Podobně nestačí, aby podmnožiny topologického prostoru byly disjunktní; chceme, aby byly (jistým způsobem) oddělené. Všechny oddělovací axiomy určitým způsobem říkají, že body nebo množiny, které jsou rozlišitelné nebo oddělené v nějakém slabším smyslu, musí také být rozlišitelné nebo oddělené v nějakém silnějším smyslu.
Nechť X je topologický prostor. Pak dva body x a y prostoru X jsou topologicky rozlišitelné, pokud nemají stejná okolí (nebo ekvivalentně stejná otevřená okolí); což znamená, že alespoň jeden z nich má okolí, které není okolím druhého (nebo ekvivalentně, že existuje otevřená množina, do které jeden bod patří a druhý ne).
Dva body x a y jsou oddělené, pokud každý z nich má okolí, které není okolím druhého; což znamená, že žádný není prvkem uzáběru druhého. Obecněji dvě podmnožiny A a B prostoru X jsou oddělené, pokud je každá disjunktní s uzávěrem druhé (samy uzávěry disjunktní být nemusí). Všechny zbývající podmínky pro separaci množin mohou být aplikovány také na body (nebo na bod a množinu) použitím jednoprvkových množin. Body x a y budeme považovat za oddělené, oddělené okolími, oddělené uzavřenými okolími, oddělené spojitou funkcí, přesně oddělené funkcí, právě tehdy, když jejich jednoprvkové množiny {x} a {y} jsou oddělené podle odpovídajících kritérií.
Podmnožiny A a B jsou oddělený okolími, pokud mají disjunktní okolí. Jsou oddělené uzavřenými okolími, pokud mají disjunktní uzavřená okolí. Jsou oddělené spojitou funkcí, pokud existuje spojité zobrazení f z prostoru X na reálnou osu R takové, že pro jejich obrazy platí, že f(A) je rovno {0} a f(B) je rovno {1}. A konečně jsou přesně odděleny spojitou funkcí, pokud existuje spojitá funkce f z X do R taková, že vzorem f−1({0}) je A a vzorem f−1({1}) je B.
Tyto podmínky jsou zde uvedeny v pořadí podle zvýšující se síly: jakékoli dva topologicky rozlišitelné body musí být různé, a jakékoli dva oddělené body musí být topologicky rozlišitelné. Jakékoli dvě oddělené množiny musí být disjunktní, jakékoli dvě množiny oddělené okolími musí být oddělené, atd.
Další informace o těchto podmínkách (včetně jejich používání mimo oddělovací axiomy) je uvedeno v článcích Oddělené množiny a Topologická rozlišitelnost.
Hlavní definice
Všechny tyto definice používají v zásadě předběžné definice uvedené výše.
Mnoho těchto názvů má u některých autorů jiný význam, jak je vysvětleno v článku Historie separačních axiomů; například význam názvů „normální“ a „T4“ jsou někdy prohozeny, podobně „regulární“ a „T3“ atd. Mnoho konceptů má několik názvů; u názvu, který uveden jako první, je nejméně pravděpodobné, že bude nejednoznačný.
Většina těchto axiomů má alternativní definice se stejným významem; zde uvedené definice tvoří konzistentním vzorek, který ukazuje souvislost různých pojmů separace definovaných v předchozí části. Jiné možné definice lze nalézt v jednotlivých článcích.
Ve všech následujících definicích je X vždy topologický prostor.
- X je T0 neboli Kolmogorovův, pokud jakékoli dva různé body v X jsou topologicky rozlišitelné. (U oddělovacích axiomů je běžné, že existuje jedna verze axiomu, která vyžaduje T0, a druhá, která to nevyžaduje.)
- X je R0 neboli symetrický, pokud jakékoli dva topologicky rozlišitelné body v X jsou oddělené.
- X je T1 neboli dostupný neboli Fréchetův neboli Tichonovův, pokud jakékoli dva různé body v X jsou oddělené. Ekvivalentně každá jednobodová množina je uzavřená. X je tedy T1 právě tehdy, když je zároveň T0 a R0. (Přestože je možné říkat takové věci jako „T1 prostor“, „Fréchetova topologie“, a „předpokládejme, že topologický prostor X je Fréchetův“; nepoužívejte v tomto kontextu název „Fréchetův prostor“, protože tento název se používá ve funkcionální analýze pro zcela odlišný objekt.)
- X je R1 neboli preregulární, pokud jakékoli dva topologicky rozlišitelné body v X jsou oddělený okolími. Každý R1 prostor je také R0.
- X je Hausdorffův neboli T2 neboli oddělený, pokud jakékoli dva různé body v X jsou oddělené okolími. X je tedy Hausdorffův právě tehdy, když je zároveň T0 a R1. Každý Hausdorffův prostor je také T1.
- X je T2½ neboli Urysohnův, pokud jakékoli dva různé body v X jsou oddělené uzavřenými okolími. Každý T2½ prostor je také Hausdorffův.
- X je úplně Hausdorffův neboli úplně T2, pokud jakékoli dva různé body v X jsou oddělené spojitou funkcí. Každý úplně Hausdorffův prostor je také T2½.
- X je regulární, pokud, je-li dán jakýkoli bod x a uzavřená množina F v X tak, že x nepatří do F, jsou oddělené okolími. (Neboli v regulárním prostoru jakákoli taková x a F budou také oddělena uzavřenými okolími.) Každý regulární prostor je také R1.
- X je regulární Hausdorffův neboli T3, pokud je T0 a regulární.[1] Každý regulární Hausdorffův prostor je také T2½.
- X je úplně regulární, pokud, je-li dán jakýkoli bod x a uzavřená množina F v X tak, že x nepatří do F, jsou oddělené spojitou funkcí. Každý úplně regulární prostor je také regulární.
- X je Tichonovův neboli T3½, úplně T3 neboli úplně regulární Hausdorffův, pokud je T0 a zároveň úplně regulární.[2] Každý Tichonovův prostor je regulární Hausdorffův a zároveň úplně Hausdorffův.
- X je normální, pokud jakékoli dvě disjunktní uzavřené podmnožiny prostoru X jsou oddělené okolími. (Neboli prostor je normální právě tehdy, když jakékoli dvě disjunktní uzavřené množiny lze oddělit spojitou funkcí; toto je Urysohnovo lemma.)
- X je normální regulární, pokud je R0 a zároveň normální. Každý normální regulární prostor je regulární.
- X je normální Hausdorffův neboli T4, pokud je T1 a zároveň normální. Každý normální Hausdorffův prostor je Tichonovův a zároveň normální regulární.
- X je úplně normální, pokud jakékoli dvě oddělené množiny jsou oddělený okolími. Každý úplně normální prostor je také normální.
- X je úplně normální Hausdorffův neboli T5 neboli úplně T4, pokud je úplně normální a zároveň T1. Každý úplně normální Hausdorffův prostor je také normální Hausdorffův.
- X je Perfektně normální, pokud jakékoli dvě disjunktní uzavřené množiny jsou přesně oddělený spojitou funkcí. Každý perfektně normální prostor je také úplně normální.
- X je Perfektně normální Hausdorffův neboli T6 neboli perfektně T4, pokud je perfektně normální a zároveň T1. Každý perfektně normální Hausdorffův prostor je také úplně normální Hausdorffův.
Následující tabulka sumarizuje oddělovací axiomy i vztahy mezi nimi: buňky které jsou sloučeny, reprezentují ekvivalentní vlastnosti, každý axiom implikuje vlastnosti v buňkách vlevo od něj, a je-li splněn axiom T1, pak každý axiom také implikuje vlastnosti v buňkách nad ním (například všechny normální T1 prostory jsou také úplně regulární).
| Oddělené | Oddělené okolími | Oddělené uzavřenými okolími | Oddělené funkcí | Přesně oddělené funkcí | |
|---|---|---|---|---|---|
| Rozlišitelné Body | Symetrický | Preregulární | |||
| Různé Body | Fréchetův | Hausdorffův | Urysohnův | Úplně Hausdorffův | Perfektně Hausdorffův |
| Uzavřená množina a bod, který do ní nepatří | (vždy splněno) | Regulární | Úplně regulární | Perfektně regulární | |
| Disjunktní uzavřené množiny | (vždy splněno) | Normální | Perfektně normální | ||
| Oddělené množiny | (vždy splněno) | úplně normální | |||
Vztahy mezi axiomy
Axiom T0 je speciální v tom smyslu, že nemůže být pouze přidán k vlastnostem (takže úplně regulární plus T0 je Tichonovův), ale musí být také odebrán od vlastností (takže Hausdorffův minus T0 je R1) ve zcela přesném smyslu; další informace jsou v článku Kolmogorovův kvocient. Aplikací na oddělovací axiomy dostaneme vztahy v tabulce vlevo dole. V této tabulce se přechází zprava doleva přidáním vlastnosti T0, a zleva doprava odstraněním tohoto požadavku pomocí operace Kolmogorovova kvocientu. (Názvy v závorkách uvedené na levé straně této tabulky jsou obecně nejednoznačné nebo alespoň méně známé; jsou však použity v grafu níže.)
| T0 verze | Non-T0 verze |
|---|---|
| T0 | (žádný požadavek) |
| T1 | R0 |
| Hausdorffův (T2) | R1 |
| T2½ | (žádné speciální jméno) |
| Úplně Hausdorffův | (žádné speciální jméno) |
| Regulární Hausdorffův (T3) | Regulární |
| Tichonovův (T3½) | Úplně regulární |
| Normální T0 | Normální |
| Normální Hausdorffův (T4) | Normální regulární |
| Úplně normální T0 | Úplně normální |
| Úplně normální Hausdorffův (T5) | Úplně normální regulární |
| Perfektně normální T0 | Perfektně normální |
| Perfektně normální Hausdorffův (T6) | Perfektně normální regulární |
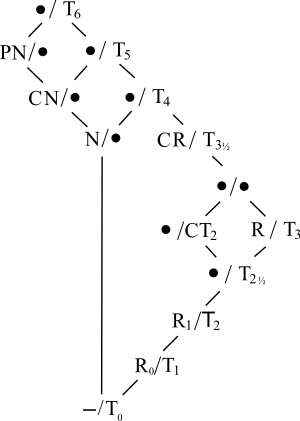
Jiné vztahy mezi oddělovacími axiomy než splňování nebo nesplňování podmínky T0 ukazuje graf vpravo. V tomto grafu je označení prostoru, který nesplňuje axiom T0 vlevo od lomítka, a označení prostoru, který axiom T0 splňuje vpravo od lomítka. Písmena vyjadřují zkratky takto: “P“ = „perfektně“, „C“ = „úplně“, „N“ = „normální“, a „R“ (bez dolního indexu) = „regulární“. Puntík znamená, že příslušný prostor nemá žádné speciální jméno. Pomlčka ve spodní části indikuje prázdnou podmínku.
Pomocí tohoto grafu je možné zkombinovat libovolné dvě vlastnosti tak, že postupujeme grafem nahoru, až se obě větve setkají. Pokud například prostor je úplně normální (“CN“) a zároveň úplně Hausdorffův (“CT2“), pak procházíme oběma větvemi vzhůru, až najdeme místo „•/T5“. Protože úplně Hausdorffovy prostory jsou T0 (přestože úplně normální prostory jimi být nemohou), vezmeme T0 stranu lomítka; úplně normální úplně Hausdorffův prostor je totéž jako T5 prostor (jednoznačněji známý jako úplně normální Hausdorffův prostor, jak je vidět v tabulce výše).
Z grafu je vidět, že normální a R0 současně znamená splnění jiných vlastností, protože kombinování dvou vlastností vyžaduje průchod pravou větví. Protože z nich je nejznámější regulárnost, prostory, které jsou normální i R0 se obvykle nazývají „normální regulární prostory“. Podobně prostory, které jsou normální i T1, se často nazývají „normální Hausdorffovy prostory“, aby se zabránilo nejednoznačnosti v „T“ notaci. Tyto konvence lze zobecnit na jiné regulární prostory a Hausdorffovy prostory.
Jiné oddělovací axiomy
Existují i jiné podmínky kladené na topologické prostory, které jsou někdy klasifikovány jako oddělovací axiomy, ty se však k obvyklým oddělovacím axiomům nedají úplně zařadit. Jiný než jejich definice zde nejsou diskutovány; viz jednotlivé jim věnované články.
- X je střízlivý, pokud pro každou uzavřenou množinu C, která není (případně nedisjunktním) sjednocením dvou menších uzavřených množin, existuje jediný bod p takový, že uzávěr jednoprvkové množiny {p} se rovná C. Stručněji každá ireducibilní uzavřená množina má jediný generický bod. Jakýkoli Hausdorffův prostor musí být střízlivý, a jakýkoli střízlivý prostor musí být T0.
- X je slabě Hausdorffův, pokud obraz každého spojitého zobrazení f na X z kompaktního Hausdorffova prostoru je uzavřený v X. Jakýkoli Hausdorffův prostor musí být slabě Hausdorffův, a jakýkoli slabě Hausdorffův prostor musí být T1.
- X je semiregulární, pokud regulární otevřené množiny tvoří bázi topologického prostoru pro otevřené množiny prostoru X. Jakýkoli regulární prostor musí také být semiregulární.
- X je kvaziregulární, pokud pro jakoukoli neprázdnou otevřenou množinu G existuje neprázdná otevřená množina H taková, že uzávěr H je obsažen v G.
- X je plně normální, pokud každé pokrytí má otevřené hvězdičkové zjemnění. X je plně T4 nebo plně normální Hausdorffův, pokud je T1 a plně normální. Každý plně normální prostor je normální a Každý plně T4 prostor je T4. Navíc můžeme ukázat, že Každý plně T4 prostor je parakompaktní. Vlastně, plně normální prostory skutečně mají více společné s parakompaktností než s obvyklými oddělovacími axiomy.
- Síla podmínky, aby všechny kompaktní podmnožiny byly uzavřené, je mezi T1 a T2 (Hausdorffův). Prostor vyhovující této podmínce je nutně T1, protože každá jednobodová množina je nutně kompaktní a tedy uzavřená, ale opačné tvrzení není nutně pravdivé; pro kofinitní topologii na nekonečně mnoha bodech, která je T1, je každá podmnožina kompaktní, ale ne každá podmnožina je uzavřená. Navíc každý T2 (Hausdorffův) prostor vyhovuje axiomu, že všechny kompaktní podmnožiny jsou uzavřené, ale opačné tvrzení není nutně pravdivé; pro kospočetnou topologii na nespočetně mnoha bodech jsou kompaktní množiny vesměs konečné a tedy všechny uzavřené, ale prostor není T2 (Hausdorffův).
Odkazy
Poznámky
- Schechter 1997, s. 441.
- Schechter 1997, s. 443.
Reference
V tomto článku byl použit překlad textu z článku Separation axiom na anglické Wikipedii.
Související články
- Obecná topologie
Literatura
- SCHECHTER, Eric, 1997. Handbook of Analysis and its Foundations. San Diego: Academic Press. Dostupné online. ISBN 0126227608. (mimo jiné definuje Ri axiomy)
- WILLARD, Stephen, 1970. General topology. Reading, Mass.: Addison-Wesley Pub. Co.. Dostupné online. ISBN 0-486-43479-6. (obsahuje všechny axiomy zmíněné v sekci Hlavní definice kromě axiomů Ri, s uvedenými definicemi)
- MERRIFIELD, Richard E.; SIMMONS, Howard E., 1989. Topological Methods in Chemistry. New York: Wiley. Dostupné online. ISBN 0-471-83817-9. (poskytuje čtivý úvod do oddělovacích axiomů s důrazem na konečné prostory)
Externí odkazy
- Separation Axioms at ProvenMath – separační axiomy na ProvenMath
- Table of separation a metrisability axioms from Schechter – Tabulka separačních axiomů z výše uvedené Schechterovy knihy