Nepřímá úměrnost
Nepřímou úměrností se nazývá každá funkce daná rovnicí , kde představuje reálné číslo různé od nuly. Definiční obor této funkce je množina všech reálných čísel různých od nuly (perioda). Grafem nepřímé úměrnosti v ortonormální souřadnicové soustavě je rovnoosá hyperbola. Osy x a y jsou asymptoty grafu této funkce.
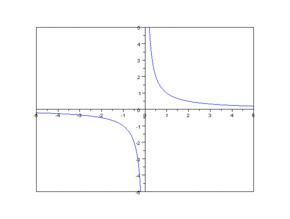
Příklad
Příkladem může být závislost času potřebného k překonání určité vzdálenosti na rychlosti. Čím vyšší rychlostí jedu, tím kratší dobu mi trvá někam dojet. Další situací může být závislost času potřebného k dokončení určitého úkolu v závislosti na počtu osob či strojů, které daný úkol zpracovávají. Čím více pracovníků, tím rychleji je práce hotova.
Vlastnosti funkce
je na intervalech a klesající pro a naopak rostoucí pro .
Poznámka
Někdy se také za nepřímou úměrnost chybně považuje i situace, kdy se nejedná o přísně přímou úměrnost. Jedná se o případy, kdy hodnota obou veličin stoupá, ale ne stejně „rychle“. Příkladem může být délka strany čtverce a jeho obsah. Jestliže se délka strany čtverce dvakrát zvětší, obsah čtverce se zvětší čtyřikrát. Pak se ale jedná o prostou úměrnost.