Nejednoznačná gramatika

Nejednoznačná gramatika (anglicky ambiguous grammar) v teorii formálních jazyků je taková bezkontextová gramatika, která generuje (aspoň jednu) nejednoznačnou větu. Nejednoznačná věta je taková věta, pro kterou existují nejméně dva různé derivační stromy.[1][2] Pokud každá z vět generovaných gramatikou má jediný derivační strom, je gramatika jednoznačná.

Nejednoznačný jazyk je jazyk, pro které neexistuje žádná jednoznačná gramatika.[1][2]

Aby se předešlo problémům s porovnáváním derivačních stromů používá se také definice, že nejednoznačná gramatika je bezkontextová gramatika, v níž existuje věta, který má více než jednu levou derivaci, zatímco jednoznačná gramatika (anglicky unambiguous grammar) je bezkontextová gramatika, jejíž každá větu má jednoznačnou levou derivaci.

Problém zjišťování nejednoznačnosti gramatiky je pro obecné bezkontextové gramatiky algoritmicky nerozhodnutelný.[1][2]

Vztah jednoznačných gramatik a jazyků

Pro mnoho jazyků existují nejednoznačné i jednoznačné gramatiky, ale pro některé jazyky existují pouze nejednoznačné gramatiky. Pro jakýkoli neprázdný jazyk lze sestrojit nejednoznačnou gramatiku z jednoznačné gramatiky přidáním duplicitních pravidel nebo synonym (jediný jazyk bez nejednoznačné gramatiky je prázdný jazyk). Jazyk, který připouští pouze nejednoznačné gramatiky, se nazývá z podstaty nejednoznačný jazyk, a z podstaty nejednoznačný bezkontextové jazyky existují. Deterministické bezkontextové gramatiky jsou vždy jednoznačné a jsou důležitou podtřídou jednoznačných bezkontextových gramatik; existují však i nedeterministické jednoznačné bezkontextové gramatiky.

Pro skutečné programovací jazyky je referenční bezkontextová gramatika často nejednoznačná, kvůli problémům jako je nepovinné else. Jsou-li takovéto nejednoznačnosti přítomny, jsou zpravidla řešeny přidáním precedenčních pravidel nebo jiných kontextových pravidel tak, aby výsledná frázová gramatika byla jednoznačná.

Příklady

Triviální jazyk

Nejjednodušším příkladem nejednoznačné gramatiky je následující gramatika triviálního jazyka, který sestává pouze z prázdného řetězce:

S → A | B
A → ε
B → ε

…což znamená, že prázdný řetězec ε může být vytvořen libovolným ze dvou ekvivalentních pravidel a tedy má dvě levé derivace.

Další nejednoznačná gramatika pro triviální jazyk je:

A → A | ε

…což znamená, že symbol A se přepíše buď na sebe sama nebo na prázdný řetězec. Pro prázdný řetězec tedy existují levé derivace délky 1, 2, 3, … Podle toho, kolikrát se použije pravidlo A → A, může mít derivace libovolnou délku.

Tento jazyk má i jednoznačnou gramatiku, obsahující pouze jedno přepisovací pravidlo:

A → ε

…což znamená, že jednoznačné přepisovací pravidlo může produkovat pouze prázdný řetězec, což je jednoznačný řetězec v jazyce.

Stejným způsobem lze z libovolné gramatiky pro neprázdný jazyk vytvořit nejednoznačnou gramatiku přidáním duplikátů.

Unární řetězec

Regulární jazyk unárních řetězců určitého znaku, např. 'a' (popsaný regulárním výrazem a*), má jednoznačnou gramatiku:

A → aA | ε

…ale má také nejednoznačnou gramatiku:

A → aA | Aa | ε

První gramatika odpovídá vytváření zprava asociativního stromu (pro jednoznačnou gramatiku), druhá dovoluje levé- i pravé- spojení. Toto je rozebráno níže.

Sčítání a odčítání

Bezkontextová gramatika

A → A + A | A − A | a

je nejednoznačná, protože pro řetězec a + a + a existují dvě levé derivace:

    A→ A + A      A→ A + A
    → a + A      → A + A + A (První A je nahrazeno řetězcem A+A. Nahrazení druhého A dává podobné odvození)
    → a + A + A      → a + A + A
    → a + a + A      → a + a + A
    → a + a + a      → a + a + a

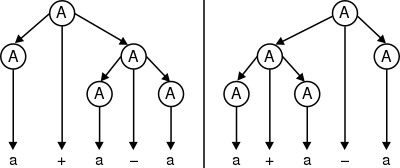
Jako jiný příklad, gramatika je nejednoznačná, protože existují dva derivační stromy pro řetězec + −:

Jazyk, který gramatika generuje, není nejednoznačný ze své podstaty; jednoznačná gramatika, která jej generuje, je:

A → A + a | A − a | a

Nepovinné else
Podrobnější informace naleznete v článku Nepovinné else.

Častým příkladem nejednoznačnosti ve skutečných programovacích jazycích je nepovinné else. V mnoha jazycích je část za else v podmíněném příkazu if-then-else nepovinná. Při vnoření dvou nebo více podmíněných příkazů do sebe není jednoznačné, ke kterém if dané else patří, přinejmenším při použití bezkontextových gramatik.

Konkrétně v mnoha jazycích lze psát podmíněný příkaz dvěma způsoby: ve tvaru if-then a ve tvaru if-then-else:

V gramatice obsahující pravidla

Příkaz =   if Podmínka then Příkaz |
           if Podmínka then Příkaz else Příkaz |
           …
Podmínka = …

se mohou objevit některé nejednoznačné frázové struktury. Výraz

if a then if b then s else s2

může být analyzován jako

if a then (if b then s) else s2

nebo jako

if a then (if b then s else s2)

podle toho, zda else má patřit k prvnímu nebo druhému if.

Tento problém se v různých jazycích řeší různě. Je možné navrhnout syntaxi programovacího jazyka tak, aby byla jednoznačná, například zakončením podmíněného příkazu klíčovým slovem endif, nebo nepovolením nepovinného else. Nebo je možné nechat bezkontextovou gramatiku nejednoznačnou, a přidat kontextové pravidlo, například že else patří k nejbližšímu if. Výsledná gramatika je pak jednoznačná, ale není bezkontextová.

Rozpoznávání nejednoznačných gramatik

Rozhodnutí, zda obecná bezkontextová gramatika je jednoznačná, je algoritmicky nerozhodnutelný problém, protože lze ukázat, že je ekvivalentní s Postovým korespondenčním problémem[3]. Existují však nástroje, které implementují různé postupy umožňující detekovat některé případy nejednoznačnosti bezkontextových gramatik.[4]

Efektivita syntaktické analýzy bezkontextové gramatiky je určena automatem, který ji přijímá. Deterministické bezkontextové gramatiky jsou přijímány deterministickými zásobníkovými automaty a mohou být analyzovány v lineárním čase, například LR analyzátorem[5]. Je to vlastní podmnožina bezkontextových gramatik, které jsou přijímány zásobníkovým automatem a mohou být analyzovány v polynomiálním čase, například CYK algoritmem. Jednoznačné bezkontextové gramatiky mohou být nedeterministické. Například jazyk palindromů sudé délky nad abecedou 0 a 1 má jednoznačnou bezkontextovou gramatiku S → 0S0 | 1S1 | ε. Libovolný řetězec tohoto jazyka nemůže být analyzován bez načtení celého řetězce, což znamená, že zásobníkový automat musí zkusit alternativní přechody mezi stavy, aby podporoval různé možné délky částečně analyzovaného řetězce.[6] Odstranění nejednoznačností gramatiky může produkovat deterministickou bezkontextovou gramatiku a tedy umožnit efektivnější syntaktickou analýzu. Generátory překladačů, jako například Yacc, obsahují prostředky pro řešení některých druhů nejednoznačnosti například pomocí precedence a omezení asociativity.

Jazyky z podstaty nejednoznačné

Existenci jazyků z podstaty nejednoznačných dokázal Rohit Parikh v roce 1961 ve výzkumné zprávě MIT[7] (Parikhova věta).

Zatímco některé bezkontextové jazyky (množiny řetězců, které lze generovat gramatikou) mají nejednoznačné i jednoznačné gramatiky, existují bezkontextové jazyky, pro které jednoznačná bezkontextová gramatika neexistuje. Příkladem ze podstaty nejednoznačného jazyka je sjednocení množin a . Výsledný jazyk je bezkontextový, protože sjednocení dvou bezkontextových jazyků je vždy bezkontextový jazyk. Ale Ullman 1979 podal důkaz, že nelze jednoznačně analyzovat řetězce v (nebezkontextové) podmnožině , která je průnikem těchto dvou jazyků[8].

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Ambiguous grammar na anglické Wikipedii.

  1. GRIES, David. Compiler Construction for Digital Computers. [s.l.]: John Wiley and Sons, Inc., 1971.
  2. GRIES, David. Compiler Construction for Digital Computers. Překlad Ľubomír Šlahor, František Pástor. Bratislava: Alfa, 1981.
  3. Hopcroft, Motwani, Ullman (2001), Věta 9.20, p.405-406
  4. AXELSSON, Roland; HELJANKO, Keijo; LANGE, Martin. Proceedings of the 35th International Colloquium on Automata, Languages and Programming (ICALP'08), Reykjavik, Iceland. Svazek 5126. [s.l.]: Springer-Verlag, 2008. (Lecture Notes v Computer Science). Dostupné online. Kapitola Analyzing Context-Free Grammars Using an Incremental SAT Solver.
  5. KNUTH, D.E. On the translation of languages from left to right. Information and Control. Červenec 1965, roč. 8, čís. 6, s. 607–639. Dostupné v archivu pořízeném dne 2012-03-15. DOI 10.1016/S0019-9958(65)90426-2.
  6. HOPCROFT, John; MOTWANI, Rajeev; ULLMAN, Jeffrey. Introduction to automata theory, languages, and computation. 2nd. vyd. [s.l.]: Addison-Wesley, 2001.
  7. PARIKH, Rohit. Language-generating devices. [s.l.]: Quarterly Progress Report, Research Laboratory of Electronics, MIT, January 1961.
  8. p.99-103, Sect.4.7
  • GROSS, Maurice. Inherent ambiguity of minimal linear grammars. Information and Control. Information and Control, September 1964. DOI 10.1016/S0019-9958(64)90422-X.
  • MICHAEL, Harrison. Introduction to Formal Language Theory. [s.l.]: Addison-Wesley, 1978. ISBN 0201029553.
  • HOPCROFT, John E.; ULLMAN, Jeffrey D., 1979. Introduction to Automata Theory, Languages, and Computation. 1. vyd. [s.l.]: Addison-Wesley.
  • HOPCROFT, John; MOWANI, Rajeev; ULLMAN, Jeffrey, 2001. Introduction to Automata Theory, Languages and Computation. 2. vyd. [s.l.]: Addison Wesley.
  • BRABRAND, Claus; GIEGERICH, Robert; MØLLER, Anders. Analyzing Ambiguity of Context-Free Grammars. Science of Computer Programming. Elsevier, March 2010. DOI 10.1016/j.scico.2009.11.002.

Související články
  • Syntaktická nejednoznačnost

Analyzátory pro nejednoznačné a nedeterministické gramatiky:

Externí odkazy
  • dk.brics.gramatika – analyzátor nejednoznačnosti gramatik.
  • CFGAnalyzer – nástroj pro analýzu bezkontextových gramatik vzhledem k algoritmicky nerozhodnutelným problémům univerzalitě, nejednoznačnosti a podobným vlastnostem jazyka (analyzátor nemusí vydat rozhodnutí v omezeném čase).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.