LR syntaktický analyzátor
LR syntaktický analyzátor (anglicky LR parser) je v matematické informatice typ syntaktického analyzátoru zdola nahoru, který efektivně zpracovává deterministické bezkontextové jazyky v zaručeném lineárním čase[1]. Jeho často používanými variantami jsou LALR analyzátor a SLR analyzátor. Pro vytváření LR syntaktických analyzátorů se často používají generátory syntaktických analyzátorů, které generují analyzátor mechanicky z formální gramatiky jazyka. Častěji než jiné druhy generovaných syntaktických analyzátorů se používají pro zpracování programovacích jazyků.
Zkratku LR, případně LR(k) lze rozložit na jednotlivé složky: L znamená, že syntaktický analyzátor čte vstupní text v jednom směru bez návratu (tak funguje většina syntaktických analyzátorů) typicky zleva doprava. R znamená, že syntaktický analyzátor provádí syntaktickou analýzu zdola nahoru a produkuje obrácený pravý rozbor, čímž se liší od velké skupiny analyzátorů provádějících syntaktickou analýzu shora dolů nebo ad-hoc. Zkratka LR je často následována číselným kvalifikátorem, např. LR(1) nebo LR(k). Aby se zamezilo backtrackingu nebo hádání, analyzátor se rozhoduje, jak analyzovat předchozí symboly, na základě náhledu na k dosud nezpracovaných vstupních symbolů. Nejčastěji bývá k rovno 1, a pak se neuvádí. Zkratku LR často předchází jiné kvalifikátory, jako SLR a LALR.
LR syntaktické analyzátory jsou deterministické; produkují jedinou správnou syntaktickou analýzu bez hádání nebo návratu (anglicky backtracking) a pracují v lineárním čase. Díky tomu jsou ideální pro programovací jazyky. Lidské jazyky jsou naproti tomu nejednoznačné a vyžadují flexibilnější metody, které však jsou pomalejší. Příkladem je CYK algoritmus, Earleyův analyzátor a GLR syntaktický analyzátor), které provádějí návraty nebo dávají více analýz, a mohou mít časovou složitost O(n2), O(n3) nebo dokonce exponenciální, pokud provádějí špatné odhady.
Výše uvedené vlastnosti L, R a k ve skutečnosti mají všechny syntaktické analyzátory založené na přístupu přesun-redukce, včetně jednoduchého precedenčního syntaktického analyzátoru. Označení LR se však používá pouze pro třídu analyzátorů, které poprvé popsal Donald Knuth, nikoli na dřívější, méně výkonné precedenční metody (například operátorový precedenční syntaktický analyzátor)[1]. LR syntaktický analyzátor může zpracovávat větší obor jazyků a gramatik než precedenční syntaktický analyzátor nebo analyzátor shora dolů[2]. Je to způsobeno tím, že syntaktický analyzátor LR má pro rozhodování, jaké pravidlo použít, k dispozici celou instanci nějakého vzorku gramatiky. LL syntaktický analyzátor se naproti tomu musí rozhodnout a odhadnout, jaké pravidlo použít, mnohem dříve, v okamžiku, kdy viděl pouze první symbol zleva v tomto vzorku. LR je také lepší v oznamování chyb. Syntaktické chyby ve vstupním proudu detekuje hned, jak je to možné.
Úvod
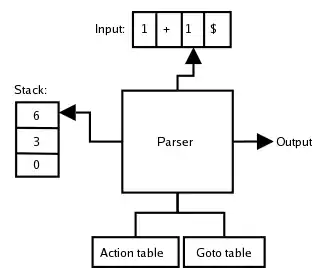
LR analyzátor načítá a analyzuje vstupní text v jednom průchodu textem zleva doprava. Derivační strom analyzátor vytváří inkrementálně, zdola nahoru a zleva doprava, bez hádání nebo backtrackingu. V každém bodě tohoto průchodu analyzátor vytváří seznam podstromů nebo frází vstupního textu, které již byly analyzovány. Tyto podstromy zatím nejsou spojeny, protože analyzátor ještě nedosáhl pravého konce syntaktického vzoru, který použije pro jejich složení.
Gramatika pro A*2 + 1
LR analyzátory se konstruují z gramatik, které formálně definují syntaxi vstupního jazyka jako množinu vzorků. Gramatika v praxi nepokrývá všechna pravidla jazyka, nezabývá se například formátováním textu programu pomocí mezer a konců řádků, velikostí čísel nebo konzistencí používání jmen a jejich definic v kontextu celého programu. LR analyzátory používají bezkontextové gramatiky, které pracují pouze s lokálními vzorky symbolů.
Použijeme malý výsek gramatiky popisující aritmetický výraz v programovacím jazyce Java nebo C:
- r0: Goal → Sums eof
- r1: Sums → Sums + Products
- r2: Sums → Products
- r3: Products → Products * Value
- r4: Products → Value
- r5: Value → int
- r6: Value → id
Terminální symboly gramatiky jsou víceznakové symboly neboli 'tokens', které ze vstupního proudu načetl lexikální analyzátor. V našem případě se jedná o symboly + * a int pro libovolnou celočíselnou konstantu, id pro libovolné jméno identifikátoru a eof pro konec vstupního souboru. Gramatika se nestará o to, jakou konkrétní hodnotu mají symboly int nebo id, ani o mezery a znaky konce řádku. Gramatika tyto terminální symboly používá, ale nedefinuje je. Jedná se vždy o koncové uzly (ve spodní části) derivačního stromu.
Slova začínající velkým písmenem jako Sums jsou neterminální symboly. Jsou to jména pro koncepty, syntaktické kategorie nebo vzorky v jazyce, které se samy ve vstupním proudu nikdy neobjeví. Jsou pouze použity v gramatice pro popis struktury jazyka. V derivačním stromě jsou to vždy interní uzly (nad spodní částí). Při analýze se objeví jako výsledek použití některého z pravidel gramatiky. Některé terminály jsou na levé straně dvou nebo více pravidel; pak se jedná o alternativní pravidla. Pravidla, ve kterých se vyskytuje stejný neterminál na levé i pravé straně, se nazývají rekurzivní. V této gramatice se rekurzivní pravidla používají pro definici opakovaných matematických operátorů. Gramatiky pro úplné jazyky používají rekurzivní pravidla pro zpracovávání seznamů, uzávorkovaných výrazů a vnořených příkazů.
Derivační strom analýzy zdola nahoru řetězce A*2 + 1
V kroku 6 v příkladu analýzy, bylo analyzováno pouze „A*2“, neúplně. Z derivačního stromu máme pouze tmavěji podbarvený spodní levý roh. Uzly od čísla 7 zatím neexistují. Uzly 3, 4 a 6 jsou kořeny izolovaných podstromů, po řadě pro proměnnou, operátor * a číslo 2. Tyto tři výchozí uzly jsou dočasně uchovávány na zásobníku analyzátoru. Zbývající nenačtená část vstupního proudu je „+ 1“.
Akce přesun a redukce
LR analyzátor se řadí k analyzátorům typu přesun-redukce, které provádějí dva druhy akcí:
- Přesun (anglicky Shift) je načtení symbolu ze vstupního proudu. Načtený symbol se stane novým derivačním stromem s jedním uzlem.
- Redukce (anglicky Reduce) aplikuje pravidlo gramatiky na několik posledních derivačních stromů, které spojí do jednoho stromu s nový počátečním symbolem.
Pokud vstup neobsahuje syntaktické chyby, analyzátor opakuje tyto kroky, dokud nenačte celý vstup a dokud všechny dílčí derivační stromy nejsou zkombinovány do jediného stromu, který reprezentuje analýzu celého vstupního řetězce.
LR analyzátory se liší od jiných analyzátorů pracujících metodou přesun-redukce tím, jak se rozhodují, kdy provést redukci a jak vybírat z pravidel s podobnými konci. Ale výsledné rozhodnutí a posloupnost přesunů a redukcí je stejná.
Efektivita LR analyzátorů pramení především z jejich determinismu. Aby LR analyzátor nemusel hádat, co dělat s dříve načtenými symboly, obvykle načítá další nezpracované symboly (výhled, anglicky lookahead). Lexikální analyzátor funguje s výhledem na jeden nebo více symbolů analyzátoru. Symboly ve výhledu jsou 'pravým kontextem' pro rozhodování o dalším postupu analýzy.[3]
Zásobník analyzátoru zdola nahoru
Stejně jako jiné analyzátory pracující metodou přesun-redukce LR analyzátory před rozhodnutím, o jakou konstrukci se jedná, čekají, dokud nejsou načteny a analyzovány všechny složky této konstrukce. Analyzátor pak hned zpracovává výslednou kombinaci. V derivačním stromu v ukázce, se v krocích 1-3 fráze A zredukuje na Value a pak na Products, jakmile se ve výhledu objeví *, a již se nečeká na pozdější kombinování těchto složek do derivačního stromu. Rozhodnutí, jak zpracovávat A závisí pouze na tom, co bylo dosud nečteno na vstupu analyzátoru, bez uvažováním symbolů, které se vyskytují dále vpravo.
Redukce reorganizuje jeden nebo více naposledy analyzovaných objektů, které jsou bezprostředně před symbolem ve výhledu. Seznam již analyzovaných objektů tedy funguje jako zásobník. Pokud obsah zásobníku analyzátoru (anglicky parse stack) zapíšeme jako řetězec, roste doprava. Dno zásobníku je tedy úplně vlevo a obsahuje nejlevější, tj. nejstarší fragment analýzy. Každá redukce pracuje pouze se symboly na pravém konci, kde jsou nejnovější fragmenty analýzy. (Tím se akumulativní zásobník LR analyzátoru výrazně liší od prediktivního, doleva rostoucího zásobníku analyzátorů provádějících analýzu shora dolů.)
Analýza zdola nahoru řetězce A*2 + 1
| Krok | Zásobník analyzátoru | Nenačteno | Akce |
|---|---|---|---|
| 0 | prázdný | A*2 + 1 | přesun |
| 1 | id | *2 + 1 | Value → id |
| 2 | Value | *2 + 1 | Products → Value |
| 3 | Products | *2 + 1 | přesun |
| 4 | Products * | 2 + 1 | přesun |
| 5 | Products * int | + 1 | Value → int |
| 6 | Products * Value | + 1 | Products → Products * Value |
| 7 | Products | + 1 | Sums → Products |
| 8 | Sums | + 1 | přesun |
| 9 | Sums + | 1 | přesun |
| 10 | Sums + int | eof | Value → int |
| 11 | Sums + Value | eof | Products → Value |
| 12 | Sums + Products | eof | Sums → Sums + Products |
| 13 | Sums | eof | přijato |
V kroku 6 se provádí redukce podle pravidla s více symboly na pravé straně:
- Products → Products * Value
které porovná vrchol zásobníku obsahující analyzovanou frázi „... Products * Value“. Redukce nahradí tuto instanci pravé strany pravidla, „Products * Value“ levou stranou, v tomto případě symbolem Products. Pokud by analyzátor vytvářel úplné derivační stromy, tři stromy pro vnitřní Products, * a Value by byly zkombinovány do nového stromu s kořenem Products. Sémantické detaily z vnitřních uzlů Products a Value jsou výstupem pro pozdější průchody překladače nebo jsou zkombinovány a uloženy do nového symbolu Products.[4]
LR kroky analýzy řetězce A*2 + 1
U slabých LR analyzátorů jsou rozhodnutí o přesunu nebo redukci založena na obsahu celého zásobníku, nejen na symbolu na vrcholu zásobníku. Nevhodná implementace by mohla vést k velmi pomalým analyzátorům, jejichž rychlost by dále klesala pro delší vstupy. Aby mohly LR analyzátory provádět rozhodnutí s konstantní rychlostí, musí sumarizovat všechny relevantní informace z levého kontextu do jediné hodnoty nazývané LR(0) stav analyzátoru (anglicky parser state). Pro každou gramatiku a metodu LR analýzy existuje pevný (konečný) počet takových stavů. Zásobník analyzátoru uchovává kromě již analyzovaných symbolů také čísla doposud dosažených stavů.
Vstupní text je v každém okamžiku analýzy rozdělen na již analyzované fráze na zásobníku, aktuální symbol ve výhledu a zbývající, dosud nenačtený, text. Další akce analyzátoru je určena aktuálním LR(0) číslem stavu (na zásobníku úplně vpravo) a symbolem ve výhledu. V následujícím textu jsou všechny informace psané černě stejné jako u jiných analyzátorů nepracujících metodou LR přesun-redukce. LR analyzátor ukládá na zásobník stavové informace zapsané fialově, přičemž sumarizuje černé fráze vlevo na zásobníku, a jaké syntaktické možnosti mají být očekávány dále. Uživatelé LR analyzátoru stavové informace obvykle ignorují. Tyto stavy jsou vysvětleny v další části.
Krok | Zásobník analyzátoru stav [Symbolstav]* | Výhled | Nenačtený vstup | Akce analyzátoru | Pravidlo gramatiky | Aktuální stav |
|---|---|---|---|---|---|---|
| 0 |
0 |
id | A*2 + 1 | přesun | 9 | |
| 1 |
0 id9 |
* | 2 + 1 | redukce | Value → id | 7 |
| 2 |
0 Value7 |
* | 2 + 1 | redukce | Products → Value | 4 |
| 3 |
0 Products4 |
* | 2 + 1 | přesun | 5 | |
| 4 |
0 Products4 *5 |
int | + 1 | přesun | 8 | |
| 5 |
0 Products4 *5 int8 |
+ | 1 | redukce | Value → int | 6 |
| 6 |
0 Products4 *5 Value6 |
+ | 1 | redukce | Products → Products * Value | 4 |
| 7 |
0 Products4 |
+ | 1 | redukce | Sums → Products | 1 |
| 8 |
0 Sums1 |
+ | 1 | přesun | 2 | |
| 9 |
0 Sums1 +2 |
int | eof | přesun | 8 | |
| 10 |
0 Sums1 +2 int8 |
eof | redukce | Value → int | 7 | |
| 11 |
0 Sums1 +2 Value7 |
eof | redukce | Products → Value | 3 | |
| 12 |
0 Sums1 +2 Products3 |
eof | redukce | Sums → Sums + Products | 1 | |
| 13 |
0 Sums1 |
eof | přijetí | |||
V počátečním kroku 0 je vstupní řetězec „A*2 + 1“ rozdělen na
- prázdnou část na zásobníku analyzátoru,
- text výhledu „A“ načtený (lexikálním analyzátorem) jako symbol id a
- zbývající dosud nenačtený text „*2 + 1“.
Na začátku analýzy obsahuje zásobník analyzátoru pouze počáteční stav 0. Pokud analyzátor ve stavu 0 vidí výhled id, musí provést přesun, který uloží symbol id na zásobník, načte další vstupní symbol * a přejde do stavu 9.
V kroku 4 je původní vstup „A*2 + 1“ rozdělen na
- analyzovanou část „A *“ se 2 frázemi ( Products a *) uloženými na zásobník,
- text výhledu „2“ načtený jako symbol int a
- zbývající dosud nenačtený text „ + 1“.
Stavy odpovídající již analyzované frázi uložené na zásobníku jsou 0, 4 a 5. Na vrcholu zásobníku (úplně vpravo) je stav 5. Pokud ve stavu 5 je výhled int, analyzátor provede přesun, který uloží int na zásobník jako samostatnou frázi, načte další vstupní symbol + a přejde do stavu 8.
V kroku 12 jsou již všechny symboly ze vstupního proudu načteny, ale ještě nejsou úplně zpracovány. Aktuální stav je 3. Pokud ve stavu 3 je výhled eof, je třeba aplikovat pravidlo gramatiky
- Sums → Sums + Products
které zkombinuje tři fráze (Sums, + a Products) na pravém konci zásobníku do jednoho symbolu. Stav 3 sám neví, jaký má být následující stav. Toto lze zjistit návratem do stavu 0, bezprostředně vlevo od fráze, která je redukována. Když je ve stavu 0 dokončena instance neterminálu Sums, přejde analyzátor do stavu 1 (opět). Kvůli tomuto udržování starších stavů, se pro jejich ukládání používá zásobníku, místo udržování pouze aktuálního stavu.
Tabulka analyzátoru pro ukázkovou gramatiku
Určitý programovací jazyk lze popsat různými gramatikami. LR(1) analyzátor může zpracovávat většinu běžných gramatik, ale ne všechny. Gramatiku lze často ručně upravit tak, aby vyhovovala omezením LR(1) analyzátoru nebo generátoru analyzátorů.
Gramatika pro LR analyzátor musí být buď sama jednoznačná nebo musí být rozšířena o rozhodovací precedenční pravidla. To znamená, že smí existovat pouze jeden správný způsob, jak aplikovat gramatiku na daný povolený ukázkový jazyk, který dává jednoznačný derivační strom s pouze jedním významem a jednoznačnou posloupností činností přesun/redukce pro daný příklad. LR analýza není vhodná pro lidské jazyky s nejednoznačnými gramatikami, které závisí na interpretaci slov. Pro lidské jazyky jsou vhodnější analyzátory jako je Zobecněný LR analyzátor, Earleyův analyzátor nebo CYK algoritmus, které umožňují vypočítat všechny možné derivační stromy v jednom průchodu.
Většina LR analyzátorů je řízena tabulkou. Algoritmus analyzátoru je jednoduchá smyčka, která nezávisí na gramatice a jazyku. Znalost gramatiky a jejích syntaktických dopadů je zakódována do pevných tabulek nazývaných tabulky analýzy (anglicky parse tables). Položky v tabulce ukazují, zda se má provést přesun nebo redukce (a podle jakého pravidla gramatiky) pro každou povolenou kombinaci stavu analyzátoru a symbol ve výhledu. Tabulky pro syntaktickou analýzu také říkají, jak vypočítat další stav z aktuálního stavu a symbolu na vstupu.
Tabulky pro syntaktickou analýzu jsou mnohem větší než gramatika. Pro velké gramatiky je obtížné sestavit LR tabulky ručně. Proto se obvykle vytvářejí mechanicky z gramatiky nějakým generátorem syntaktických analyzátorů, jako je Bison.[5]
Podle toho, jak se vytvářejí stavy a tabulka pro analýzu, výsledný analyzátor se nazývá buď SLR (jednoduchý LR) analyzátor (anglicky SLR), LALR (LR analyzátor s náhledem) (anglicky LALR), anebo kanonický LR analyzátor. LALR analyzátor lze sestrojit pro větší třídu gramatik než SLR analyzátory. Kanonické LR analyzátory zpracovávají ještě rozsáhlejší třídu gramatik, ale mají daleko více stavů a mnohem větší tabulky. Gramatika z příkladu je SLR.
LR tabulky analyzátoru jsou dvourozměrné. Tabulka LR(0) analyzátoru má jeden řádek pro každý stav. Každý vstupní symbol má vlastní sloupec. Některé kombinace stavu a dalšího symbolu nejsou pro povolené vstupní proudy možné. Tato prázdná políčka znamenají oznámení syntaktické chyby.
Levá polovina tabulky, Action, obsahuje sloupce pro terminální symboly ve výhledu. Políčka v této části tabulky určují, zda další akce analyzátoru bude přesun (do stavu n) nebo redukce (podle pravidla rn).
Pravá polovina tabulky, Goto, obsahuje sloupce pro neterminální symboly. Políčka v této části ukazují, do kterého stavu přejít po redukci podle pravidla, které má na levá straně určitý neterminální symbol. Tato část tabulky funguje jako akce přesunu, ale pro neterminály; terminální symboly ve výhledu nejsou změněny.
Sloupec „Aktuální pravidla“ ukazuje význam a syntaktické možnosti pro jednotlivé stavy tak, jak je vytvořil generátor syntaktických analyzátorů. Během analýzy nejsou tato pravidla potřebná. Značka • (růžová tečka) ukazuje místo uvnitř některého částečně rozpoznaného pravidla, v němž je analyzátor v daném okamžiku. Symboly vlevo od • již byly načteny a analyzovány, zatímco symboly vpravo od značky budou analyzovány později. Pokud analyzátor ještě nezúžil spektrum možností na jediné pravidlo, bude stav obsahovat několik takových pravidel.
| Curr | Výhled | levá strana Goto | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Stav | Aktuální pravidla | int | id | * | + | eof | Sums | Products | Value | |
| 0 | Goal → • Sums eof | 8 | 9 | 1 | 4 | 7 | ||||
| 1 | Goal → Sums • eof Sums → Sums • + Products | 2 | přijato | |||||||
| 2 | Sums → Sums + • Products | 8 | 9 | 3 | 7 | |||||
| 3 | Sums → Sums + Products • Products → Products • * Value | 5 | r1 | r1 | ||||||
| 4 | Sums → Products • Products → Products • * Value | 5 | r2 | r2 | ||||||
| 5 | Products → Products * • Value | 8 | 9 | 6 | ||||||
| 6 | Products → Products * Value • | r3 | r3 | r3 | ||||||
| 7 | Products → Value • | r4 | r4 | r4 | ||||||
| 8 | Value → int • | r5 | r5 | r5 | ||||||
| 9 | Value → id • | r6 | r6 | r6 | ||||||
Ve stavu 2 výše, analyzátor právě nalezl a přesunul + z pravidla
- r1: Sums → Sums + • Products
Další očekávaná fráze je Products. Products začíná terminálním symbolem int nebo id. Jestliže náhled obsahuje jeden z nich, analyzátor provede přesun a přejde do stavu 8 nebo 9. Když bylo nalezeno Products, analyzátor přejde do stavu 3 pro získání úplného seznamu sčítanců a hledá konec pravidla r0. Products může také začínat neterminálem Value. Pro každý jiný výhled anebo neterminál analyzátor oznámí syntaktickou chyba.
Ve stavu 3 analyzátor právě nalezl frázi Products, která mohla vzniknout ze dvou možných pravidel gramatiky:
- r1: Sums → Sums + Products •
- r3: Products → Products • * Value
Mezi r1 a r3 nelze rozhodnout pouze podle analýzy předchozí fráze. Analyzátor musí použít výhled, aby rozhodl, kterou akci má provést. Jestliže výhled je *, jsme v pravidle 3, a analyzátor provede přesun * a přejde do stavu 5. Jestliže výhled je eof, jsme na konci pravidla 1 a 0, a analýza končí.
Ve stavu 9 výše, obsahují všechna neprázdná políčka, v nichž není chyba, redukci r6. Některé analyzátory šetří čas a prostor tabulky tak, že v těchto jednoduchých případech nekontrolují výhled. Syntaktické chyby jsou pak detekovány poněkud později, po některé neškodné redukci, ale stále před další akcí přesunu nebo rozhodnutím analyzátoru.
Jednotlivá políčka tabulky nesmí obsahovat více možností, jinak by analyzátor byl nedeterministický a musel by používat backtracking. Jestliže gramatika není LR(1), některá políčka budou obsahovat konflikty přesun/redukce mezi akcemi přesunu a redukce nebo konflikty redukce/redukce mezi více pravidly gramatiky. Tyto konflikty řeší LR(k) analyzátory (pokud je to možné) kontrolou dalších symbolů ve výhledu za prvním symbolem.
Smyčka LR analyzátoru
Při zahájení analýzy obsahuje zásobník LR analyzátoru pouze počáteční stav 0; výhled obsahuje první symbol načtený ze vstupního proudu. Analyzátor pak opakuje následující kroky ve smyčce, dokud neskončí nebo nenarazí na syntaktickou chybu:
Stav na vrcholu zásobníku analyzátoru označíme s a terminální symbol, který je ve výhledu označíme t. Další akci analyzátoru najdeme v řádku s a sloupci t tabulky Výhled Action. Touto akcí může být Přesun, Redukce, Přijetí nebo Chyba:
- Přesun n:
- Přesuň první terminál t z výhledu na zásobník analyzátoru a načti další vstupní symbol do paměti výhledu.
- Na zásobník analyzátoru ulož další stav n jako nový aktuální stav.
- Redukce rm: Použij pravidlo gramatiky rm: X → S1 S2 ... SL
- Odstraň L symbolů (a derivační stromy a příslušná čísla stavů) z vrcholu zásobníku analyzátoru.
- Tím se odkryje předchozí stav p, který byl očekáván instancí symbolu na levé straně pravidla.
- Spoj L derivačních stromů do jednoho derivačního stromu, který bude mít v kořeni symbol z levé strany pravidla.
- Vyhledej další stav n v řádku p a sloupci odpovídajícímu symbolu X na levé straně pravidla v levé straně Goto tabulky.
- Na zásobník analyzátoru ulož symbol z levé strany pravidla a odpovídající strom.
- Na zásobník analyzátoru ulož další stav n jako nový aktuální stav.
- Výhled a vstupní proud se nemění.
- Přijetí: Pokud výhled t je značka eof, ukonči analýzu. Pokud zásobník stavů obsahuje pouze počáteční stav, oznam úspěch. Jinak oznam syntaktickou chybu.
- Žádná akce: Oznam syntaktickou chybu. Analýza končí nebo se analyzátor snaží zotavit z chyb a pokračovat v analýze.
Poznámka: na zásobník LR analyzátoru se obvykle ukládají pouze stavy LR(0) automatu, protože symboly gramatiky z nich lze odvodit (v automatu jsou všechny vstupní přechody do některého stavu označeny stejným symbolem, jako je symbol spojený s tímto stavem). Navíc tyto symboly nejsou téměř nikdy potřebné, protože při rozhodování o dalším kroku analýzy záleží pouze na stavu.[6]
LR generátory analýzátorů
Tuto část článku může většina uživatelů LR generátorů analyzátorů přeskočit.
LR stavy
Stav 2 v ukázce tabulky analyzátoru odpovídá částečně analyzovanému pravidlu
- r1: Sums → Sums + • Products
Je zřejmé, jak se sem analyzátor dostal: nejdříve viděl Sums a pak +, když hledal větší Sums. Značku • přesunul za začátek pravidla. Také je vidět, jak analyzátor čeká na ukončení úplného pravidla, dalším hledáním úplného Products. Jsou však potřebné další detaily, aby bylo možné analyzovat všechny složky tohoto Products.
Částečně analyzovaná pravidla pro určitý stav nazýváme „jádrové LR(0) položky“ (anglicky core LR(0) items) stavu. Generátor analyzátorů přidává dodatečná pravidla nebo položky pro všechny další kroky při vytváření očekávaného Products:
- r3: Products → • Products * Value
- r4: Products → • Value
- r5: Value → • int
- r6: Value → • id
Všimněte si, že značka • je na začátku každého z těchto přidaných pravidel; analyzátor ještě nemá potvrzenu ani analyzovánu žádnou část z nich. Tyto přídavné položky se nazývají „uzávěr“ jádrových položek. Pro každý neterminální symbol bezprostředně následující •, generátor přidává pravidla definující tento symbol. Tím se přidává více značek • a případně různé následující symboly. Proces výpočtu uzávěru pokračuje, dokud nejsou expandované všechny následující symboly. Následující neterminály pro stav 2 začínají symbolem Products. Do uzávěru se pak přidá symbol Value. Následující terminály jsou int a id.
Položky jádra a uzávěru ukazují všechny možné povolené cesty zpracování z aktuálního stavu do budoucích stavů a úplné fráze. Pokud se následník objevuje pouze v jedné položce, vede k dalšímu stavu, který obsahuje pouze jednu jádrovou položku s posunutou značkou •. int tedy vede k dalšímu stavu 8 s jádrem
- r5: Value → int •
Pokud se v několika položkách objevuje stejný následující symbol, analyzátor zatím nemůže rozhodnout, které pravidlo má použít. Tento symbol tedy vede k dalšímu stavu, který ukazuje všechny zbývající možnosti, opět s posunutou značkou •. Products se objevuje v r1 i r3. Proto Products vede k dalšímu stavu 4 s jádrem
- r1: Sums → Sums + Products •
- r3: Products → Products • * Value
Jinak řečeno, znamená to, že pokud analyzátor viděl jediný symbol Products, jeho analýza může končit nebo mohou následovat další hodnoty které se budou spolu násobit. Všimněte si, že všechny jádrové položky mají před značkou • stejný symbol; všechny přechody do tohoto stavu jsou se stejným symbolem.
Některé přechody vedou do jader a stavů, které jsme již viděli. Jiné přechody vedou do nového stavu. Generátor začíná výchozím pravidlem gramatiky. Z něho stále hledá známé stavy a přechody, dokud neprojde všechny potřebné stavy.
Tyto stavy se nazývají „LR(0)“ stavy, protože používají výhled s k=0, tj. žádný výhled. Jediná kontrola vstupních symbolů se objeví, když je symbol načítán. Kontrola výhledu pro redukce se provádí odděleně pomocí tabulky analyzátoru, ne samotnými vyjmenovanými stavy.
Konečný automat
Tabulka analyzátoru popisuje všechny možné LR(0) stavy a přechody mezi nimi. Stavy tvoří konečný automat (FSM). Konečný automat je jednoduchý stroj pro analýzu jednoduchých nerekurzivních jazyků bez použití zásobníku. Při použití pro LR analýzu obsahuje „vstupní jazyk“ konečného automatu terminální i neterminální symboly gramatiky a pokrývá všechny snímky částečně analyzovaného zásobníku plné LR analýzy.
Vraťme se ke kroku 5 analýzy v příkladu:
Krok | Zásobník analyzátoru stav Symbol stav ... | Výhled | Nenačteno |
|---|---|---|---|
| 5 |
0 Products4 *5 int8 |
+ | 1 |
Zásobník analyzátoru ukazuje posloupnost změn stavů z počátečního stavu 0 do stavu 4 a dále do stavu 5 a aktuálního stavu 8. Na zásobníku analyzátoru jsou symboly přesun nebo goto. Další způsob prohlížet toto, je, že konečný automat může načíst proud „Products * int + 1“ (zatím bez použití dalšího zásobníku) a najde nejlevější úplnou frázi, která musí být redukována příště. To je opravdu jeho úloha!
Jak je možné, že na tento úkol stačí obyčejný konečný automat, když analyzovaný jazyk obsahuje vnořování a rekurzi a určitě vyžaduje analyzátor se zásobníkem? Vysvětlením je, že vše vlevo od vrcholu zásobníku už bylo plně zredukované. To z těchto frází odstraňuje všechny smyčky a vnořování. Konečný automat může ignorovat všechny starší začátky frází a sledovat pouze nejnovější fráze, které mohou být dokončeny příště. V teorii se pro tento řetězec nazývá perspektivní předpona (anglicky viable prefix).
Výhledové množiny
Všechny informace potřebné pro konstrukci tabulky analyzátoru lze získat z množiny stavů a z přechodové funkce. Generátor také potřebuje vypočítat očekávané výhledové množiny (anglicky lookahead sets) pro každou akci redukce.
U SLR analyzátorů lze výhledové množiny určit přímo z gramatiky bez uvažováním jednotlivých stavů a přechodů. SLR generátor vytvoří pro každý neterminál S množinu Follows(S) obsahující všechny terminální symboly, které mohou bezprostředně následovat nějaký výskyt symbolu S. V parse tabulce každá redukce na S používá Follow(S) jako LR(1) výhledovou množinu. Tyto Follow množiny používají i generátory LL analyzátorů shora dolů. Gramatika, která neobsahuje žádné konflikty přesun/redukce nebo redukce/redukce při použití množiny Follow, se nazývá SLR gramatika.
LALR analyzátory mají stejné stavy jako SLR analyzátory, ale používají složitější a přesnější způsob zjišťování minimálních nezbytných náhledů pro redukce pro každý stav. V závislosti na detailech gramatiky může být výsledek stejný jako množina Follow vypočítaná SLR generátorem analyzátorů nebo se může jednat o podmnožinu SLR výhledů. Některé gramatiky jsou vhodné pro LALR generátory analyzátorů ale ne pro SLR generátory analyzátorů. Stává se to u gramatik, u kterých se při použití množin Follow objevují nepravé konflikty přesun/redukce nebo redukce/redukce, ale žádné konflikty při použití množin vypočítaných LALR generátorem. Gramatika se pak nazývá LALR(1), a není SLR.
SLR a LALR analyzátory nemají duplicitní stavy. Tato minimalizace však není nezbytná a někdy může způsobovat zbytečné výhledové konflikty. Kanonické LR (anglicky Canonical LR) analyzátory používají zdvojené (nebo „rozdělené“) stavy pro lepší zapamatování levého a pravého kontextu neterminálů používá. Každý výskyt symbol S v gramatice můžeme uvažovat nezávisle s vlastní výhledové množina, pro vyřešení konfliktů při redukci. Díky tomu zpracovává mnohem více gramatik. Toto řešení však vede k mnohem větším tabulkám analyzátorů, pokud se provede pro všechny složky gramatiky. Rozštěpení stavů lze také provést ručně a selektivně pro libovolný SLR nebo LALR analyzátor vytvořením dvou nebo více pojmenovaných kopií některých neterminálů. Gramatika, která je bezkonfliktní pro kanonický LR generátor, ale má konflikty pro LALR generátor, se nazývá LR(1) gramatika, a není LALR(1) ani SLR gramatikou.
Při zpracování řetězců, které patří do jazyka, provádějí SLR, LALR a kanonické LR analyzátory úplně stejná rozhodnutí mezi přesunem a redukcí. Když však vstup obsahuje syntaktickou chybu, může LALR analyzátor před detekováním chyby provést nějaké přídavné (neškodné) redukce, které kanonický LR analyzátor neprovádí. SLR analyzátor může těchto redukcí udělat ještě více. Dochází k tomu proto, že SLR a LALR analyzátory používají bohatou nadmnožinu přiblížení ke skutečnosti, minimální symbol ve výhledu pro tento určitý stav.
Zotavení ze syntaktických chyb
LR analyzátory mohou generovat užitečné chybové zprávy pro první syntaktickou chybu v programu vyhodnocením všech terminálních symbolů, které se mohly objevit místo neočekávaného špatného symbolu ve výhledu. To však analyzátor nepomůže rozhodnout, jak analyzuje zbytek vstupního textu programu pro nalezení další nezávislé chyby. Jestliže se analyzátor špatně zotaví z první chyby, bude s velkou pravděpodobností špatně analyzovat vše ostatní a produkovat kaskádu neužitečných falešných chybových zpráv.
Analyzátor vytvořený generátory syntaktických analyzátorů yacc nebo bison obsahuje ad hoc mechanismy pro ukončení aktuálního příkazu, zahození některých analyzovaných frází a symbolů z výhledu kolem chyby a resynchronizovat analýzu na některém spolehlivém oddělovač na úrovni příkazu, jako jsou středníky nebo složené závorky. Tento mechanismus často funguje tak dobře, že umožňuje, aby analyzátor a překladač zkontroloval zbytek programu.
Mnoho syntaktických chyby jsou jednoduché překlepy nebo vynechávky triviálního symbolu. Některé LR syntaktické analyzátory se snaží tyto případy detekovat a automaticky opravit. Analyzátor vyhodnotí každé možné vložení, smazání nebo nahrazení jednoho symbolu v místě chyby. Překladač vyzkouší analýzu s každou změnou, aby zjistil, zda opravuje chybu. (To vyžaduje backtracking na obsahu zásobníku analyzátoru a vstupní proud, normálně potřebné pro analyzátor.) Některá z nejlepších oprav je vybrána. To dává velmi užitečné chybové zprávy a dobře resynchronizuje analýzu. Oprava však není dostatečně spolehlivá, aby se podle ní mohl opravit vstupní soubor. Zotavení ze syntaktických chyb je nejsnazší provádět konzistentně v analyzátorech (jako LR), které mají parse tabulky a explicitní datový zásobník.
Varianty LR syntaktických analyzátorů
LR generátor syntaktických analyzátorů rozhoduje, co se musí stát pro každou kombinaci stavu analyzátoru a symbolu ve výhledu. Tato rozhodnutí jsou obvykle uspořádána do pevné tabulky, která řídí smyčku obecného analyzátoru. Algoritmus analyzátoru nezávisí na gramatice a stavech. Existují i jiné způsoby, jak zkonstruovat skutečný analyzátor.
Některé generátory LR analyzátorů místo parse tabulek vytvářejí zvlášť upravený programový kód pro každý stav. Tyto analyzátory mohou běžet několikrát rychleji než obecné analyzátory řízené tabulkou. Nejrychlejší analyzátory generují program v jazyce symbolických adres.
V analyzátorech s rekurzivním vzestupem je explicitní zásobník analyzátoru nahrazena implicitním zásobníkem používaným při volání podprogramů. Redukce znamenají ukončení několika úrovní volání podprogramu, což je ve většině programovacích jazyků neohrabané. Poroto jsou analyzátory s rekurzivním vzestupem obecně pomalejší, méně intuitivní a obtížněji se ručně modifikují než analyzátory s rekurzivním sestupem.
Další varianta nahrazuje parse tabulku porovnáváním vzorků v neprocedurálních jazycích, jako je například Prolog.
Zobecněné LR analyzátory (anglicky Generalized LR parsers), GLR, používají LR techniky zdola nahoru pro hledání ne jedné, ale všech možných analýz vstupního textu. To je nezbytné pro nejednoznačné gramatiky, které se vyskytují při zpracování přirozených jazyků. Tyto analyzátory vytvářejí současně více povolených derivačních stromů bez backtrackingu. GLR může být užitečné pro programovací jazyky, které nelze snadno popsat LALR(1) gramatikou bez konfliktů.
Left corner analyzátory (LC) používají LR techniky zdola nahoru pro rozpoznávání levého konce alternativních pravidel gramatiky. Když existuje pouze jedna alternativa (jedno možné pravidlo), analyzátor pak pro analýzu zbytku tohoto pravidla přepne na techniku LL(1) shora dolů. LC analyzátory mají menší parse tabulky než LALR analyzátory a lepší chybovou diagnostiku. Pro deterministické LC analyzátory neexistuje šířeji používaný generátor. LC analyzátory vracející více analýz jsou užitečné pro lidské jazyky s velmi rozsáhlými gramatikami.
Teorie
LR analyzátory vynalezl Donald Knuth v roce 1965 jako efektivní zobecnění precedenčních analyzátorů. Knuth dokázal, že LR analyzátory jsou víceúčelové analyzátory, které jsou efektivní i pro nejhorší možný případ.
- „LR(k) gramatiky lze efektivně analyzovat v čase přímo úměrném délce řetězce.“[7]
- Pro každé k≥1, „lze jazyk generovat LR(k) gramatikou právě tehdy, když je tento jazyk deterministický [a bezkontextový], právě tehdy, když jej lze generovat LR(1) gramatikou.“[8]
Jinými slovy, jestliže jazyk byl významné dostatečně umožnit efektivní jednoprůchodový analyzátor, lze jej popsat LR(k) gramatikou. Tuto gramatika lze vždy mechanicky transformovat na ekvivalentní (ale větší) LR(1) gramatiku. Tedy metoda LR(1) analýzy by teoreticky měla být dostatečně výkonná pro zpracování libovolného významného jazyka. V praxi se přirozené gramatiky mnoha programovacích jazyků příliš neodchylují od LR(1).
Kanonické LR analyzátory popsané Knuthem měly příliš mnoho stavů a rozsáhlé tabulky analyzátorů, příliš velké pro omezenou paměť tehdejších počítačů. LR analýza se začala prakticky používat poté, co Frank DeRemer vynalezl SLR a LALR analyzátor s mnohem menším počtem stavů.[9][10]
Detaily teorie LR jazyků a způsob, jak se LR analyzátory vytvářejí z gramatik popisuje kniha Theory of Parsing, Translation and Compiling, Volume 1 (Aho and Ullman)[6][11].
Earleyův analyzátor používá techniky a • notace LR analyzátorů pro generování všech možných analýz pro nejednoznačné gramatiky, ke kterým patří například lidské jazyky.
Zatímco LR(k) gramatiky mají stejnou sílu pro všechna k≥1, síla LR(0) gramatik se nepatrně liší. O jazyce L řekneme, že má prefixovou vlastnost, jestliže žádné slovo v L není vlastním prefixem jiného slova v L.[12] Pro jazyk L existuje LR(0) gramatika právě tehdy, když L je deterministický bezkontextový jazyk s prefixovou vlastností.[13] Důsledkem toho je jazyk L deterministický bezkontextový právě tehdy, když pro L$ existuje LR(0) gramatika, ve které „$“ není symbolem z abecedy jazyka L[14].
Další příklad 1+1
Tento příklad LR analýzy používá následující malou gramatiku s počátečním symbolem E:
- (1) E → E * B
- (2) E → E + B
- (3) E → B
- (4) B → 0
- (5) B → 1
pro analýzu následujícího vstupu:
- 1 + 1
Tabulky action a goto
Obě tabulky pro LR(0) analýzu této gramatiky lze znázornit takto:
| stav | akce | goto | |||||
| * | + | 0 | 1 | $ | E | B | |
| 0 | s1 | s2 | 3 | 4 | |||
| 1 | r4 | r4 | r4 | r4 | r4 | ||
| 2 | r5 | r5 | r5 | r5 | r5 | ||
| 3 | s5 | s6 | acc | ||||
| 4 | r3 | r3 | r3 | r3 | r3 | ||
| 5 | s1 | s2 | 7 | ||||
| 6 | s1 | s2 | 8 | ||||
| 7 | r1 | r1 | r1 | r1 | r1 | ||
| 8 | r2 | r2 | r2 | r2 | r2 | ||
Action tabulka (anglicky action table) je indexovaná stavem analyzátoru a terminálem (včetně speciálního terminálu $, který indikuje konec vstupního proudu) a obsahuje tři typy činností:
- přesun, zapisovaný jako 'sn', který indikuje, že další stav je n
- redukce, zapisovaná jako 'rm', která indikuje, že je třeba provést redukci pomocí pravidla m gramatiky
- přijetí zapisované jako 'acc' indikuje, že analyzátor vstupní řetězec přijímá.
Goto tabulka (anglicky goto table) je indexovaná stavem analyzátoru a neterminálem a jednoduše indikuje, jaký bude další stav analyzátoru, jestliže rozpoznal určitý neterminál. V této tabulka se vyhledává další stav po každé redukci. Po redukci najdeme další stav v goto tabulce pro položku na vrcholu zásobníku (tj. aktuální stav) a levou stranu pravidla použitého při redukci (tj. neterminál).
Kroky analýzy
Následující tabulka ukazuje jednotlivé kroky analýzy. Stav znamená prvek na vrcholu zásobníku (prvek úplně vpravo). Další akce je určena odkazem do action tabulka výše. Všimněte si, že na konec vstupního řetězce je přidán symbol $ označující konec vstupu.
| Stav | Vstupní proud | Výstupní proud | Zásobník analyzátoru | Aktuální akce |
|---|---|---|---|---|
| 0 | 1+1$ | [0] | Přesun 2 | |
| 2 | +1$ | [0,2] | Redukce 5 | |
| 4 | +1$ | 5 | [0,4] | Redukce 3 |
| 3 | +1$ | 5,3 | [0,3] | Přesun 6 |
| 6 | 1$ | 5,3 | [0,3,6] | Přesun 2 |
| 2 | $ | 5,3 | [0,3,6,2] | Redukce 5 |
| 8 | $ | 5,3,5 | [0,3,6,8] | Redukce 2 |
| 3 | $ | 5,3,5,2 | [0,3] | Přijetí |
Průběh analýzy
Analyzátor začíná se zásobníkem obsahujícím pouze počáteční stav ('0'):
- [0]
První symbol ze vstupního řetězce, který analyzátor vidí, je '1'. Pro zjištění, jakou další akci provést (přesun, redukce, přijetí nebo chyba), je action tabulka indexovaná aktuálním stavem (pamatujte, že „aktuální stav“ je pouze symbol na vrcholu zásobníku), který v tomto případě je 0 a aktuální vstupní symbol, který je '1'. Action tabulka určuje přechod do stavu 2, a proto je stav 2 uložen na zásobník (opět pamatujte, že všechny informace o stavu jsou na zásobníku, takže „přesun do stavu 2“ je totéž jako uložení 2 na zásobník). Výsledný zásobník je
- [0 '1' 2]
kde vrchol zásobníku je 2. Kvůli přehlednosti je zobrazen symbol (např. '1' nebo B), který způsobil přechod do dalšího stavu, i když tento symbol na zásobníku není.
Ve stavu 2 action tabulka říká, že bez ohledu na to, jaký terminál analyzátor vidí ve vstupním proudu, musí provést redukci podle pravidla 5. Je-li tabulka správná, znamená to, že analyzátor právě rozpoznal pravou stranu pravidla 5, což je skutečně náš případ. V tomto případě analyzátor zapíše 5 do výstupního proudu, vyzvedne jeden stav ze zásobníku (protože pravá strana pravidla má jeden symbol) a uloží na zásobník stav z goto tabulky z políčka pro stav 0 a B, tj. stav 4. Výsledný zásobník je:
- [0 B 4]
Ve stavu 4 však action tabulka říká, že analyzátor musí nyní provést redukci podle pravidla 3. Proto zapíše 3 do výstupního proudu, vyzvedne jeden stav ze zásobníku a v goto tabulce najde nový stav pro stav 0 a symbol E, což je stav 3. Výsledný zásobník je:
- [0 E 3]
Další terminál, který analyzátor vidí, je '+', a podle action tabulky musí přejít do stavu 6:
- [0 E 3 '+' 6]
Všimněte si, že výsledný zásobník lze interpretovat jako historii konečného automatu, který načetl pouze neterminál E následovaný terminálem '+'. Přechodová tabulka tohoto automatu je definovaná přesunem v action tabulce a činností goto v goto tabulce.
Další terminál je nyní '1' a to znamená, že analyzátor provede přesun a přejde do stavu 2:
- [0 E 3 '+' 6 '1' 2]
Tato jednička bude bude stejně jako předchozí redukována na B, což dává následující zásobník:
- [0 E 3 '+' 6 B 8]
Opět si všimněte, že zásobník odpovídá seznamu stavů konečného automatu, který načetl neterminál E následovaný symbolem '+', a pak neterminál B. Ve stavu 8 provádí analyzátor vždy redukci podle pravidla 2. Všimněte si, že tři stavy na vrcholu zásobníku odpovídají třem symbolům na pravé straně pravidla 2.
- [0 E 3]
Nakonec analyzátor načte '
Konstrukce LR(0) analýzu tabulky
Položky
Konstrukce těchto tabulek analýzy je založena na pojmu LR(0) položka (dále nazývaných jenom položka), což jsou pravidla gramatiky se speciální značkou-tečkou přidanou někam do pravé strany. Například k pravidlu E → E + B existují následující čtyři položky:
- E → • E + B
- E → E • + B
- E → E + • B
- E → E + B •
K pravidlům tvaru A → ε existuje pouze jediná položka A → •. Položka E → E • + B znamená, že analyzátor ve vstupním proudu právě rozpoznal řetězec odpovídající E a nyní očekává symbol '+' následovaný jiným řetězcem, který odpovídá B.
Množiny položek
Protože ne vždy víme předem, jaké pravidlo se použije pro redukci, stav analyzátoru není vždy možné charakterizovat jedinou položkou. Pokud například existuje také pravidlo E → E * B, pak se položky E → E • + B a E → E • * B uplatní po načtení řetězce odpovídajícího neterminálu E. Proto je třeba stav analyzátoru charakterizovat celou množinou položek, v tomto případě množinou { E → E • + B, E → E • * B }.
Rozšiřování množiny položek expanzí neterminálů
Položka s tečkou před neterminálem, jako například E → E + • B, indikuje, že analyzátor očekává, že bude následovat analýza neterminálu B. Aby se zajistilo, že množina položek bude obsahovala všechna možná pravidla, která analyzátor potřebuje během analýzy, je třeba do množiny položek zahrnout všechny položky, které popisují, jak bude analyzováno B. To znamená, že pokud existují pravidla jako například B → 1 a B → 0, pak množina položek musí obsahovat také položky B → • 1 a B → • 0. Obecně to lze formulovat takto:
- Jestliže množina položek obsahuje položku tvaru A → v • Bw a v gramatice existuje pravidlo tvaru B → w' , pak v množině položek musí také být položka B → • w' .
Uzávěr množiny položek
Libovolnou množinu položek je třeba tedy rozšiřovat rekurzivním přidáváním všech vhodných položek, až projdeme všechny neterminály, kterým předchází tečka. Rozšíření, které obsahuje všechny takové položky a žádné jiné, se nazývá uzávěr množiny položek; označujeme jej clos(I), kde I je množina položek. Stavy analyzátoru jsou pak reprezentovány těmito uzavřenými množinami položek, i když by stačilo uvažovat pouze ty položky, které jsou dosažitelné z počátečního stavu.
Rozšířená gramatika
Před určováním přechodů mezi stavy rozšíříme gramatiku o pravidlo
- (0) S → E
kde S je nový počáteční symbol a E původní počáteční symbol. Analyzátor použije toto pravidlo pro redukci v okamžiku, kdy přijímá celý vstupní řetězec.
V našem příkladu bude gramatika rozšířena takto:
- (0) S → E
- (1) E → E * B
- (2) E → E + B
- (3) E → B
- (4) B → 0
- (5) B → 1
Množiny položek a přechody mezi nimi budou určovány pro tuto rozšířenou gramatiku.
Konstrukce tabulek
Hledání dosažitelných množin položek a přechodů mezi nimi
Prvním krokem při konstrukci tabulek je zjištění přechodů mezi uzavřenými množinami položek. Tyto přechody zjistíme tak, že budeme uvažovat konečný automat, který může číst terminály i neterminály. Počátečním stavem tohoto automatu bude vždy uzávěr první položky přidaného pravidla: S → • E:
- Množina položek 0
- S → • E
- přidaná: E → • E * B
- přidaná: E → • E + B
- přidaná: E → • B
- přidaná: B → • 0
- přidaná: B → • 1
Položky začínající slovem přidaná: byly přidány při konstrukci uzávěru. Ostatní položky nazýváme jádro množiny položek.
Vyjdeme z počátečního stavu (S0) a určíme všechny stavy, které lze dosáhnout z počátečního stavu. Možné přechody pro množinu položek lze nalézt kontrolou symbolů (terminálů i neterminálů), které následují za tečkou; v případě množiny položek 0 jsou těmito symboly terminály '0' a '1' a neterminály E a B. Pro nalezení množiny položek, ke kterému každý symbol x vede, provedeme následující procedura pro každý symbol:
- Nechť S je podmnožina všech položek v aktuální množině položek, v nichž je značka před symbolem x, který nás zajímá.
- Pro každou položku v S, přesuneme tečku vpravo od x.
- Uzavřeme výslednou množinu položek.
Pro terminál '0' (tj. pro x = '0') dostáváme:
- Množina položek 1
- B → 0 •
a pro terminál '1' (tj. pro x = '1') dostáváme:
- Množina položek 2
- B → 1 •
a pro neterminál E (tj. pro x = E) dostáváme:
- Množina položek 3
- S → E •
- E → E • * B
- E → E • + B
a pro neterminál B (tj. pro x = B) dostáváme:
- Množina položek 4
- E → B •
Všimněte si, že uzávěr nepřidává nové položky ve všech případech - v nových množinách výše například neexistují žádné neterminály následující za tečkou. Tento proces pokračuje, dokud lze přidávat nové množiny položek. Množiny položek 1, 2 a 4 neobsahují přechody, protože tečka není před žádný symbol. Pro množinu položek 3, si všimněte, že tečka je před terminály '*' a '+'. Pro '*' dostáváme:
- Množina položek 5
- E → E * • B
- + B → • 0
- + B → • 1
a pro '+' dostáváme:
- Množina položek 6
- E → E + • B
- + B → • 0
- + B → • 1
Pro množinu položek 5, je nutné uvažovat terminály '0' a '1' a neterminál B. Pro terminály, si všimněte, že výsledné uzávěry množiny položek jsou rovné už nalezeným množinám položek 1 případně 2. Pro neterminál B dostáváme:
- Množina položek 7
- E → E * B •
Pro množinu položek 6, je nutné uvažovat terminál '0' a '1' a neterminál B. Stejně jako dříve, množiny položek pro terminály jsou rovné už nalezeným množinám položek 1 a 2. Pro neterminál B dostáváme:
- Množina položek 8
- E → E + B •
Tato poslední množina položek neobsahuje žádné symboly za tečkou, takže se nebudou přidávat žádné nové množiny položek, a procedura generování položek tak končí. Konečný automat, jehož stavy jsou tvořeny množinami položek, je ukázán níže.
Přechodová tabulka automatu nyní vypadá takto:
| Množina položek | * | + | 0 | 1 | E | B |
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | ||
| 1 | ||||||
| 2 | ||||||
| 3 | 5 | 6 | ||||
| 4 | ||||||
| 5 | 1 | 2 | 7 | |||
| 6 | 1 | 2 | 8 | |||
| 7 | ||||||
| 8 |
Konstrukce tabulek action a goto
Z této tabulky a nalezené množiny položek lze zkonstruovat tabulky action a goto takto:
- Sloupce pro neterminály jsou zkopírovány do tabulky goto.
- Sloupce pro terminály jsou zkopírovány do tabulky action jako akce přesun.
- Do action tabulky přidáme zvláštní sloupec pro symbol '
Čtenář si může ověřit, že tyto výsledky jsou skutečně v action a goto tabulkách, které byly uvedeny dříve.
Porovnání LR(0), SLR a LALR analýzy
Všimněte si, že pouze krok 4 výše uvedené procedury produkuje akce redukce, takže všechny akce redukce musí zabírat celý řádek tabulky, což znamená, že redukce bude provedena bez ohledu na další symbol ve vstupním proudu. Díky tomu se jedná o LR(0) tabulky analýzy: pro rozhodnutí, kterou redukci provést, není nutný žádný výhled (tj. výhled má délku nula). Gramatika, která potřebuje výhled pro zjednoznačnění redukce by vyžadovala řádek parse tabulky obsahující v různých sloupcích různé akce redukce, výše uvedená procedura však není schopna takové řádky vytvářet.
Existují zjemnění postupu konstrukce LR(0) tabulek (jako například SLR a LALR), která umožňují konstruovat akce redukce, které nezabírají celé řádky. Díky tomu mohou analyzovat širší třídu gramatik než LR(0) analyzátory.
Konflikty ve zkonstruovaných tabulkách
Automat konstruujeme tak, aby byl deterministický. Při přidávání akcí redukce do action tabulky se však může stát, že jedno políčko obsahuje redukci i přesun (konflikt přesun-redukce) nebo několik různých redukcí (konflikt redukce-redukce). Lze však ukázat, že pokud to nastane, gramatika není LR(0) gramatikou. Klasickým příkladem skutečného konfliktu přesun-redukce je problém nepovinného else.
Následující gramatika není LR(0) kvůli konfliktu přesun-redukce:
- (1) E → 1 E
- (2) E → 1
Množiny položek pro tuto gramatiku obsahují:
- Množina položek 1 (anglicky Item set 1)
- E → 1 • E
- E → 1 •
- + E → • 1 E
- + E → • 1
V této množině položek je konflikt přesun-redukce, protože políčko v action tabulce pro tuto množinu položek a terminál '1' obsahuje akci přesun do stavu 1 a zároveň akci redukce podle pravidla 2.
Následující příklad ukazuje gramatiku, která kvůli konfliktu redukce-redukce není LR(0):
- (1) E → 1
- (2) E → B 2
- (3) → 1
- (4) B → 1
V tomto případě získáme následující množinu položek:
- Množina položek 1 (anglicky Item set 1)
- → 1 •
- B → 1 •
Tato množina položek obsahuje konflikt redukce-redukce, protože políčko v action tabulce pro tuto množinu položek obsahuje akci redukce pro pravidlo 3 i pro pravidlo 4.
Oba výše uvedené příklady lze vyřešit tak, že analyzátor bude používat množinu FOLLOW (viz LL analyzátor) neterminálu A pro rozhodnutí, zda se použije jedno z pravidel s A na levé straně pro redukci; analyzátor použije pravidlo A → w pro redukci pouze tehdy, když další symbol ve vstupním proudu je v množině FOLLOW symbolu A. Toto řešení dává tak zvaný Jednoduchý LR analyzátor.
Související články
- Kanonický LR analyzátor
- Jednoduchý LR
- LALR analyzátor
- Zobecněný LR
Reference
V tomto článku byl použit překlad textu z článku LR parser na anglické Wikipedii.
- KNUTH, Donald E., 1965. On the translation of languages from left to right. Information and Control. Roč. 8, čís. 6. Dostupné v archivu pořízeném dne 2012-03-15. DOI 10.1016/S0019-9958(65)90426-2.
- Jazykově teoretické porovnání LL a LR gramatik
- Keith Cooper a Linda Torczon: Engineering Compiler (2. vydání), Morgan Kaufman 2011.
- Crafting a Compiler, by Charles Fischer, Ron Cytron a Richard LeBlanc, Addison Wesley 2009.
- Flex & Bison: Text Processing Tools, by John Levine, O'Reilly Media 2009.
- Compilers: Principles, techniques, and Tools (2nd Edition), by Alfred Aho, Monica Lam, Ravi Sethi, and Jeffrey Ullman, Prentice Hall 2006.
- Knuth (1965), p.638
- Knuth (1965), p.635. Knuth zde nezmiňuje omezení k≥1, které je ale vyžadováno větami, na které se odkazuje, viz strana 629 a 630. Také omezení na bezkontextové jazyky je tiše chápáno z kontextu.
- Praktický Translators pro LR(k) Languages, by Frank DeRemer, MIT PhD disertaci 1969.
- Simple LR(k) Grammars, by Frank DeRemer, Comm. ACM 14:7 1971.
- Teorie of Parsing, Translation and Compiling, Volume 1: Parsing, by Alfred Aho and Jeffrey Ullman, Prentice Hall 1972.
- HOPCROFT, John E.; ULLMAN, Jeffrey D. Introduction to Automata Theory, Languages, and Computation. [s.l.]: Addison-Wesley, 1979. Dostupné online. ISBN 0-201-02988-X. Zde: Exercise 5.8, p.121.
- Hopcroft, Ullman (1979), Věta 10.12, p.260
- Hopcroft, Ullman (1979), Důsledek p.260
Literatura
- Chapman, Nigel P., LR Parsing: Theory and Practice, Cambridge University Press, 1987. ISBN 0-521-30413-X
- Pager, D., A Practical General Method for Constructing LR(k) Parsers. Acta Informatica 7, 249 - 268 (1977)
- "Compiler Construction: Principles and Practice" by Kenneth C. Louden. ISBN 0-534-93972-4
Externí odkazy
- dickgrune.com, Parsing Techniques - A Practical Guide 1st Ed. web page of book includes downloadable pdf.
- Parsing Simulator This simulator is used to generate parsing tables LR and to resolve the exercises of the book
- Internals of an LALR(1) parser generated by GNU Bison - Implementation issues
- Course notes on LR parsing
- Shift-reduce and Reduce-reduce conflicts in an LALR parser
- A LR parser example
- Practical LR(k) Parser Construction
- The Honalee LR(k) Algorithm