Konsumpční křivka (hydrologie)

Konsumční (též konsumpční) neboli měrná křivka je vztah mezi vodním stavem na měrném objektu nebo ve vodním toku a objemovým průtokem vody tímto objektem či tokem[1][2][3][4]. Podle typu měrného objektu může být konsumční křivka stanovena analyticky (např. v případě měrných přelivů, žlabů a pod.) nebo empiricky, na základě statistického zpracování řady měření za různých vodních stavů (např. pro limnigrafickou stanici). Empirická konsumční křivka mívá oproti analytické křivce jistá specifika (hysterezi, sezónnost a pod.).

Analytická měrná křivka

Typickým příkladem analytické konsumční křivky může být např. měrná křivka často používaného měrného obdélníkového přelivu s boční kontrakcí (Ponceletova přelivu), kde je jednoznačný vztah mezi přepadovou výškou $h$ [m] a průtokem $Q$ [m³s⁻¹] dán rovnicí (viz např. [5]):

$Q=mb{\sqrt {2g}}h^{3/2}$

kde $m$ [-] je tzv. součinitel přepadu, $b$ [m] délka přelivné hrany a $g$ [ms⁻²] tíhové zrychlení.

Součinitel přepadu je pro tento typ přelivu dosti složitou funkcí přepadové výšky $h$ , délky přelivné hrany $b$ , šířky přívodního koryta $B$ [m] v hladině před přelivem a výšky přelivné hrany nade dnem $s$ [m], nebo poměru průtočné plochy koryta $S$ [m²] a průtočné plochy ve výřezu přelivu $S_{0}$ [m²]:

$m=f{\biggl (}h;{b \over B};{S_{0} \over S}{\biggr )}$ .

Empirická měrná křivka

Konsumční křivka

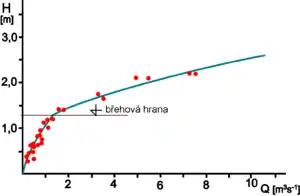
Empirická měrná křivka[4] se konstruuje pro převážnou většinu vodoměrných profilů na vodních tocích. Pro její spolehlivé vytvoření je zapotřebí větší množství dat; z toho plyne, že základní vlastností vodoměrného profilu musí být jeho stabilita, aby data byla co možná homogenní. Data se standardně získávají měřením průtoku (zpravidla hydrometrováním) za různých vodních stavů; rozsah vodních stavů při měření je žádoucí co nejširší, extrapolace měrných křivek nebývají příliš spolehlivé. Získané dvojice vodní stav $H$ [m] – průtok $Q$ [m³s⁻¹] se vynášejí do grafu $Q=f(H)$ v souřadnicích kartézských nebo často i logaritmických (v nich se níže uvedená křivka zobrazuje jako přímka) a statistickými metodami vyrovnávají křivkou, obvykle o rovnici[3][4]:

$Q=a(H-H_{0})^{c}$

kde $H_{0}$ [m] je vodní stav při nulovém průtoku a $a$ [-] a $c$ [-] jsou empirické součinitele. Pokud je tvar koryta složitější, případně za zvýšených vodních stavů (povodní) dochází k vybřežení, může mít konsumční křivka několik úseků popsaných samostatnými rovnicemi. Koncové body těchto dílčích úseků na sebe samozřejmě musí navazovat.

Kromě vlastní konsumční křivky je vhodné ze získaných dat zpracovat další závislosti typu $S=f(H)$ kde $S$ [m²] je průtočná plocha, $O=f(H)$ kde $O$ [m] je omočený obvod, případně i $R=f(H)$ kde $R$ [m] je hydraulický poloměr. Dále jsou žádoucí křivky $v=f(H)$ kde $v$ [ms⁻¹] je střední průřezová rychlost, a $n=f(H)$ kde $n$ [m^1/6] je součinitel drsnosti. Mnohdy jsou užitečné i další závislosti, např. $v_{sp}=f(H)$ kde $v_{sp}$ [ms⁻¹] je střední povrchová rychlost, která je využitelná např. za povodní pro měření plovákovou metodou. Tyto další křivky jsou užitečné zejména pro kontrolu stability a dalších vlastností měrného profilu, a pro případnou extrapolaci konsumční křivky.

Sezónní závislost

V korytech vodních toků dochází během roku k přirozeným změnám – na jaře začíná vzrůst submerzní i ripariánní vegetace, které ovlivňují hydraulické odpory a tím i závislost průtoku na vodním stavu (viz např. Chézyho rovnice a Chézyho rychlostní součinitel). Vegetace dosahuje největšího rozsahu a hustoty během léta, pak zase mizí. V zimě může dojít k zámrzu, v některých úsecích toků se může tvořit dnový led, který jednak značně ovlivňuje průtočný profil (který ledem zarůstá), jednak podstatně zvyšuje hydraulickou drsnost koryta[6]. Z těchto důvodů může být nutné vyhodnotit několik konzumčních křivek pro různá roční období, resp. různý stav koryta.

Hystereze konsumční křivky

Při větší a rychlejší změně vodního stavu se oproti ustálenému stavu (který se běžně mlčky předpokládá) mění sklon hladiny a současně dochází i ke změně průtoku, takže se mění sklon čáry energie. To ovšem znamená, že na čele průtokové (např. povodňové) vlny jistému vodnímu stavu odpovídá větší průtok než za téhož stavu při ustáleném proudění. Na sestupné větvi průtokové vlny je situace opačná – sklon hladiny je menší než za ustáleného proudění a tudíž stejnému vodnímu stavu jako za ustáleného proudění odpovídá menší průtok (viz Chézyho rovnice). Z toho též vyplývá, že maximální průtok nenastává za maximálního vodního stavu, ale ještě před jeho dosažením, a průtok za maximálního vodního stavu je menší než průtok maximální.

Extrapolace konsumční křivky

Malá extrapolace není obvykle problém; pro kontrolu správnosti lze použít pomocné křivky zkonstruované spolu s křivkou konsumční (viz výše). Správnost extrapolace lze ověřit na bázi dat získaných za povodní. Protože za větších povodní je měření průtoku zpravidla velmi problematické až zcela vyloučené, využívá se k určení povodňového průtoku tzv. povodňových značek – stop zanechaných vodou v terénu, na stromech, stavbách a pod. Tyto značky zachycují polohu hladiny při maximálním vodním stavu; vzhledem k nejistotám určení parametrů potřebných k výpočtu průtoku se na rozdíl mezi maximálním průtokem a průtokem při maximálním vodním stavu nebere zřetel.

V terénu se vytyčí a zaměří nejméně dva příčné profily, ze známé polohy povodňových značek v profilu se určí omočený obvod a průtočná plocha v každém profilu. Ze známé polohy povodňových značek v jednotlivých profilech se nivelací stanoví sklon hladiny za maximálního vodního stavu, a dále se odhadne součinitel drsnosti v jednotlivých úsecích měrné trati. Výpočet průtoku se provede metodou, odvozenou z metody pro výpočet podélného profilu hladiny ustáleného nerovnoměrného proudění(viz např. [5] pro dva zaměřené příčné profily):

$Q={\sqrt {{\Delta H} \over {\xi {\Bigl (}{1 \over {S_{d}^{2}}}-{1 \over {S_{h}^{2}}}{\Bigr )}+{l \over {R_{p}S_{p}^{2}C_{p}^{2}}}}}}$

kde $\Delta H$ [m] je rozdíl hladin v horním a dolním profilu, $\xi$ [-] ztrátový součinitel, $S_{d}$ [m²] a $S_{h}$ [m²] jsou průtočné plochy vdolním a horním profilu, a $R_{p}$ [m], $S_{p}$ [m²] a $C_{p}$ [m^0,5s⁻¹] jsou hodnoty hydrulického poloměru, průtočné plochy a Chézyho rychlostního součinitele určené jako aritmetický průměr z hodnot v horním a dolním profilu.

Reference

Dub, O., Němec, J. a kol. (1969): Hydrologie. TP34. SNTL Praha
Kříž, V. a kol.(1988): Hydrometrie. SPN Praha
Kemel, M. (1991): Hydrologie. Skripta FSv ČVUT. Praha
- (2010): Manual On Stream Gauging. Vol. II - Computation Of Discharge. WMO-1044. WMO, Geneva
Boor, B., Kunštátský, J. a Patočka, C. (1968): Hydraulika pro vodohospodářské stavby. SNTL/Alfa Praha/Bratislava
Matoušek, V. (2004): Ledový režim vodních toků. Práce a studie. VÚV Praha

Externí odkazy

Obrázky, zvuky či videa k tématu Konsumpční křivka na Wikimedia Commons

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Dub, O., Němec, J. a kol. (1969): Hydrologie. TP34. SNTL Praha

[2] Kříž, V. a kol.(1988): Hydrometrie. SPN Praha

[:0-3] Kemel, M. (1991): Hydrologie. Skripta FSv ČVUT. Praha

[:2-4] - (2010): Manual On Stream Gauging. Vol. II - Computation Of Discharge. WMO-1044. WMO, Geneva

[:1-5] Boor, B., Kunštátský, J. a Patočka, C. (1968): Hydraulika pro vodohospodářské stavby. SNTL/Alfa Praha/Bratislava

[6] Matoušek, V. (2004): Ledový režim vodních toků. Práce a studie. VÚV Praha