Harmonická řada (hudba)

Harmonická řada je posloupnost celočíselných násobků základní frekvence.

Harmonická řada kmitající struny, u níž vzdálenosti uzlů jsou úměrné převrácené hodnotě frekvence.
Prvních osm harmonických frekvencí tónu C. Zahrát současně

Laděné hudební nástroje s určitou výškou tónu nejčastěji používají přibližně harmonický oscilátor jako je struna nebo sloupec vzduchu, který kmitá na mnoha frekvencích současně. Vlny se ve struně nebo vzduchovém sloupci šíří oběma směry a většinou se vzájemně vyruší vinou destruktivní interference. Zůstanou pouze tzv. stojaté vlny, které splňují určitou speciální podmínku rezonance. Například u flétny musí mít na jednom konci uzel a na druhém kmitnu. Ve struně zase musí mít na obou koncích uzly, jak je naznačeno na obrázku vpravo. Interakcí s okolním vzduchem vznikají slyšitelné zvukové vlny, které se šíří z nástroje. Kvůli typickému rozsahu rezonancí jsou tyto frekvence většinou omezené na celočíselné násobky, neboli harmonické nejnižší frekvence a tvoří harmonickou řadu (viz harmonická řada).

Výška tónu je vnímaná vlastnost tónu, která obvykle závisí na frekvenci základní složky. Vnímaná výška tónu v hudbě je obvykle nejnižší přítomná harmonická (základní frekvence), což může být frekvence vytvořená kmitáním plné délky struny nebo vzduchového sloupce, anebo vyšší harmonická vybraná hráčem. Relativní síla jednotlivých harmonických určuje barvu zvuku setrvalého tónu nástroje.

Terminologie

Složka, harmonická, základní, neharmonická a alikvotní tón

V prvním přiblížení můžeme tón považovat za akustický signál s periodickým průběhem. Každý periodický signál „lze popsat jako kombinaci mnoha jednoduchých periodických vln (tj. sinusového průběhu) neboli složek, z nichž každá má vlastní frekvenci, amplitudu a fázi“[1].

Většina hudebních nástrojů vydává složené tóny. Složený tón je kombinací mnoha jednoduchých sinusových složek, z nichž každá má vlastní frekvenci, amplitudu a fázi vibrací (viz Fourierova analýza).

Složka je libovolný sinusový signál („jednoduchý tón“), z nichž je složen tón.

Harmonická složka (nebo jen harmonická) je taková složka, jejíž frekvence je celočíselným násobkem společné základní frekvence[2]. Do této sady patří i základní složka, jejíž frekvence je také celočíselným násobkem (jednonásobkem) sebe sama.

Neharmonická složka je každá složka, jejíž frekvence není ideálně harmonická. Neharmoničnost je míra odchylky složky od nejbližší ideální harmonické, typicky měřená v centech pro každou složku[3].

Laděné hudební nástroje s určitou výškou tónu jsou navrženy tak, aby vydávaly tóny, jejichž složky jsou téměř harmonické, s velmi nízkou neharmoničností; proto v hudební teorii a při ladění hudebních nástrojů je obvyklé říkat o složkách zvuků těchto nástrojů, že zní jako harmonické, i když mají určitou neharmoničnost. Zvuk ostatních laděných nástrojů, především některých bicích nástrojů jako marimba, vibrafon, trubicové zvony a tympány sice obsahují neharmonické složky, ale vytvářejí dobrou představu o výšce. Nástroje neladěné nebo s neurčitou výškou tónu, jako činely, gongy, nebo tam-tamy vydávají zvuky, které jsou bohaté na neharmonické složky.

Alikvotní tón je libovolná složka kromě nejnižší. Alikvotní tóny nezpůsobují harmoničnost nebo neharmoničnost a nemají žádný zvláštní význam kromě vynechaného základního tónu. To může vést ke zmatení při číslování alikvotních tónů a harmonických; první alikvotní tón je druhá harmonická.

Některé elektronické nástroje, jako thereminy a syntetizéry, vydávají tóny se sinusovým průběhem bez alikvotních tónů; syntetizéry však obvykle kombinují frekvence do složitějších tónů, aby napodobily jiné nástroje. Také některé flétny a okaríny vydávají tóny téměř bez alikvotních tónů.

Frekvence, vlnové délky a hudební intervaly v ukázkových systémech

Pro vizualizaci je nejjednodušší kmitající struna, jako na obrázku; struna je připevněna na obou koncích a každý harmonický mód ji rozděluje na 1, 2, 3, 4, atd., stejně velkých částí rezonujících na zvyšujících se frekvencích.[4] Podobné argumenty platí pro kmitající vzduchové sloupce u dechových nástrojů, i když u nich je situace komplikována existencí anti-uzlů (pro vzduchový sloupec uzavřený na jednom konci a otevřený na druhém), kuželové vrtání oproti válcovému, nebo uzavřené konce, které mění výsledný gamut od žádného, přes válcový až po exponenciálně tvarovaný (jak je patrné u různých zvonů).

U většiny laděných hudebních nástrojů je základní tón (první harmonická) doprovázen dalšími harmonickými o vyšších frekvencích. To znamená, že se ve zvuku objevují kratší vlny s vyšší frekvencí a s různou silou, které propůjčují každému nástroji charakteristickou barvu tónu. U struny, která je připevněna na obou koncích, bude nejdelší dovolené délka vlny (která určuje základní frekvenci) dvojnásobkem délky struny (polovina periody se právě vejde mezi uzly na obou koncích). Ostatní možné vlnové délky jsou 1/2, 1/3, 1/4, 1/5, 1/6, atd. násobky základní.

Tyto kratší vlnové délky teoreticky odpovídají kmitání na frekvencích, které jsou 2, 3, 4, 5, 6, atd. násobkem základní frekvence, fyzikální charakteristiky kmitajícího média a rezonátoru však tyto frekvence obvykle poněkud mění (viz neharmoničnost a roztažené ladění pro změny specifické pro nástroje s drátěnými strunami a některé elektrofonické nástroje.) Tyto změny jsou však poměrně malé, a kromě přesného, vysoce specializovaného ladění, je rozumné považovat frekvence harmonické řady za celočíselné násobky základní frekvence.

Harmonická řada v hudbě je matematicky aritmetickou řadou (1×f, 2×f, 3×f, 4×f, 5×f, ...). Vyjádřeno frekvencemi (měřenými v hertzech (Hz), kde f je základní frekvence), je rozdíl mezi sousedními harmonickými konstantní a rovný základní frekvenci. Protože však náš sluch nevnímá frekvenci zvuku lineárně, vnímáme vyšší harmonické jako vzájemně „bližší“. Naopak oktávová řada je geometrickou posloupností (2×f, 4×f, 8×f, 16×f, ...), u které člověk vnímá intervaly jako „stejně velké“. Vzhledem k našemu vnímání frekvencí je každá vyšší oktáva v harmonické řadě rozdělena na více „menších“ intervalů.

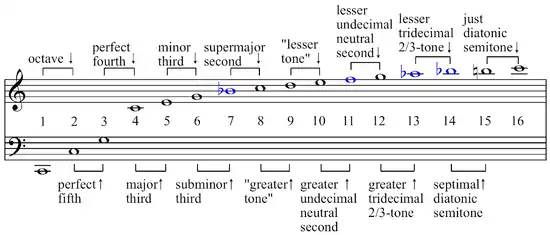
Druhá harmonická (neboli první alikvotní tón) má dvojnásobnou frekvenci než základní tón a zní o oktávu výše; třetí harmonická s frekvencí rovnou trojnásobku základního tónu zní o čistou kvintu výše než druhá. Čtvrtá harmonická kmitá na čtyřnásobku frekvence základního tónu a zní o čistou kvartu nad třetí (tj. dvě oktávy nad základním tónem). Zdvojnásobení harmonického čísla znamená zdvojnásobení frekvence (což dává o oktávu vyšší tón).

Zobrazení harmonické řady v hudební notaci. Čísla nad jednotlivými tóny ukazují odchylku od rovnoměrně temperovaného tónu v centech zaokrouhlenou na celá čísla. U not zobrazených barevně je odchylka poměrně velká; u modrých dolů, u červených nahoru.
První až 32. harmonická tónu C Přehrát
Harmonická řada v hudební notaci s označenými intervaly mezi harmonickými. Tóny vyznačené modře se výrazněji liší od rovnoměrně temperovaného ladění. Můžete si poslechnout A2 (110 Hz) a 15 jejích složek.
Notace složek 1, 3, 5, 7, 11, 13, 17 a 19 tónu C.[5] Přehrát

Harmonie a ladění

Pokud transponujeme harmonické do rozsahu jediné oktávy, blíží se některým tónům, které jsou v západní hudbě používány jako chromatická stupnice začínající základním tónem. Kvůli pevně naladěným nástrojům se v západní hudbě rozšířilo rovnoměrně temperované ladění, v němž je chromatická stupnice tvořena dvanácti stejně velkými půltóny, které jsou oproti harmonickým tónům poněkud rozladěné, zvláště v případě 7., 11. a 13. harmonické. Na konci 30. let 20. století hudební skladatel Paul Hindemith seřadil hudební intervaly podle jejich relativní disonance podle těchto a podobných harmonických vztahů.

Následující tabulka porovnává prvních 31 harmonických transponovaných do rozsahu jedné oktávy s intervaly 12-tónového rovnoměrně temperovaného ladění (12TET). Podbarvená pole zvýrazňují rozdíly větší než 5 centů (1/20 půltónu), což je přibližně nejmenší rozdíl postřehnutelný lidským uchem pro tóny hrané postupně (pokud tóny znějí současně, jsou rozpoznatelné i menší odchylky).

Harmonická 12tET Interval Tón Odchylka centů
124816prima (oktáva)C0
17malá sekundaC#, Db+5
918velká sekundaD+4
19malá tercieD#, Eb−2
51020velká tercieE−14
21kvartaF−29
1122tritónF#, Gb−49
23+28
361224kvintaG+2
25malá sextaG#, Ab−27
1326+41
27velká sextaA+6
71428malá septimaA#, B−31
29+30
1530velká septimaH−12
31+45

Frekvence harmonické řady jsou celočíselnými násobky základní frekvence, které spolu přirozeně souvisí díky celočíselným poměrům frekvencí jednotlivých složek. Tóny, jejichž složky lze vyjádřit jako poměr malých celých čísel, jsou zřejmě základem konsonance hudebních intervalů (viz čisté ladění). Tato objektivní struktura je zesílena psychoakustickými jevy. Například čistá kvinta s frekvencemi 200 a 300 Hz (cyklů za sekundu), způsobuje, že posluchač vnímá složený tón o kmitočtu 100 Hz (rozdíl 300 Hz a 200 Hz); tedy o oktávu pod nižším (skutečně znějícím) tónem. Tento kombinovaný tón prvního řádu o frekvenci 100 Hz dále interaguje s oběma tóny intervalu a vytváří složené tóny druhou řádu o frekvenci 200 (300 – 100) a 100 (200 – 100) Hz a také všechny další kombinované tóny n-tého řádu jsou stejné, tvořené různými rozdíly frekvencí 100, 200 a 300. Naproti tomu u disonantního intervalu jako je tritón (netemperovaný) s poměrem frekvencí 7:5 dostáváme frekvence 700 – 500 = 200 (kombinovaný tón 1. řádu) a 500 – 200 = 300 (2. řádu). Zbytek kombinovaných tónů jsou oktávy frekvence 100 Hz, takže interval 7:5 ve skutečnosti obsahuje 4 tóny: 100 Hz (a jejich oktávy), 300 Hz, 500 Hz a 700 Hz. Všimněte si, že nejnižší kombinovaný tón (100 Hz) je 17. (2 oktávy a velkou tercii) pod nižším (skutečně znějícím) tónem tritónu.Paul Hindemith podobně analyzuje všechny intervaly ve své knize The Craft of Musical Composition.

Barva zvuku hudebního nástroje

Relativní amplitudy (síly) různých harmonických primárně určují barvu zvuku jednotlivých nástrojů a zvuků, ale svou roli také hrají náběhové tranzienty, formanty, šumy a neharmoničnost. Například klarinet a saxofon mají podobnou hubičku a plátek a oba vytváří zvuk rezonancí vzduchu uvnitř těla nástroje, který lze považovat za uzavřený u hubičky. Avšak protože rezonátor klarinetu je válcový, jsou potlačeny sudé harmonické, což vytváří čistší tón; rezonátor saxofonu je kuželovitý, což dovoluje sudým harmonickým znít silněji, a proto vznikají složitější tóny. Neharmonické ozvy kovového rezonátoru nástroje jsou ještě více přítomné ve zvucích žesťových nástrojů.

Lidský sluch se snaží sloučit frekvence harmonicky příbuzných složek do jednoho vjemu. Lidé nevnímají jednotlivé harmonické hudební tóny samostatně, ale dohromady jako barvu tónu, přičemž vnímaná výška tónu závisí na základní frekvenci. Pokud slyšíme zvuk složený z několika frekvencí, a pokud intervaly mezi jednotlivými tóny tvoří část harmonické řady, mozek se snaží sloučit tento počitek na vjem jednoho tónu, jehož výška je určena základní frekvencí řady, i když základní tón není přítomen.

Vnímaný základní tón může také ovlivnit variace frekvence harmonické složky. Tyto variace, které jsou nejlépe zdokumentované u klavíru a jiných strunných nástrojů, ale jsou dobře patrné i u žesťových nástrojů, jsou způsobeny kombinací tuhosti kovu a interakcí kmitajícího vzduchu nebo struny s rezonančním tělem nástroje. V případě činelu velmi složitá kombinace silných vyšších alikvotních tónů a kovově cinkající zvuky téměř úplně překrývají jeho základní tón.

Síla intervalů

David Cope (1997) navrhuje koncept síly intervalů,[6], ve kterém je síla intervalů, konsonance a stabilita (viz disonance) dána přiblížením k nižší a silnější nebo vyšší a slabší pozici v harmonické řadě. Viz též Lippsův–Meyerův zákon.

Díky tomu je rovnoměrně temperovaná čistá kvinta ( přehrát) silnější než rovnoměrně temperovaná malá tercie ( přehrát), protože se blíží čisté kvintě ( přehrát), případně malé tercii ( přehrát). Malá tercie se objevuje mezi 5. a 6. harmonickou, zatímco čistá kvinta už mezi 2. a 3. harmonickou.

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Harmonic series (music) na anglické Wikipedii.

  1. THOMPSON, William Forde. Music, Thought, and Feeling: Understanding the Psychology of Music. [s.l.]: [s.n.], 2008. Dostupné online. ISBN 978-0-19-537707-1.
  2. PIERCE, John R. Music, Cognition, and Computerized Sound. [s.l.]: MIT Press, 2001. Dostupné online. ISBN 978-0-262-53190-0. Kapitola Consonance and Scales.
  3. The Historical Harpsichord Volume Two: The Metallurgy of 17th- and 18th- Century Music Wire. [s.l.]: Pendragon Press, 1987. Dostupné online. ISBN 978-0-918728-54-8.
  4. ROEDERER, Juan G. The Physics and Psychophysics of Music. [s.l.]: [s.n.], 1995. ISBN 0-387-94366-8.
  5. Fonville, John. 1991. "Ben Johnston's Extended Just Intonation: A Guide for Interpreters", p.121. Perspectives of New Music 29, no. 2 (Summer): 106–37.
  6. Cope, David (1997). Techniques of the Contemporary Composer, p.40–41. New York, New York: Schirmer Books. ISBN 0-02-864737-8.

Související články
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.