Binární vyhledávací strom

Vyhledání konkrétní hodnoty v binárním vyhledávacím stromu typicky probíhá rekurzivně. Začíná zpravidla v kořeni. V každém kroku porovná hledanou hodnotu s klíčem zkoumaného uzlu. Pokud jsou si rovny, hodnota byla nalezena. Je-li hledaná hodnota menší, pokračuje hledání v levém podstromu. Je-li větší, bude hledání pokračovat v pravém podstromu. Díky uspořádání stromu je cesta k hledané hodnotě jednoznačně určena.

Může dojít k situaci, kdy vyhledávací algoritmus narazí na neexistující uzel (dotyčný podstrom je prázdný). V takovém případě strom hledanou hodnotu neobsahuje, jinde být nemůže.

Zde je vyhledávací algoritmus v programovacím jazyce Python:

def search_binary_tree(node, key):
   if node is None:
       return None  # klíč nebyl nalezen
   elif key < node.key:
       return search_binary_tree(node.left, key)
   elif key > node.key:
       return search_binary_tree(node.right, key)
   else:  # klíč je ekvivalentní s klíčem uzlu
       return node.value  # klíč nalezen

Časová složitost vyhledávání závisí na hloubce stromu. V průměrném případě má logaritmickou časovou složitost O(log n), ale pokud je strom nevyvážený a podobá se seznamu, může mít i lineární časovou složitost O(n). Otázka správného vyvážení je z tohoto pohledu kritická a řeší ji například AVL-strom.

Vložení nového uzlu začíná hledáním jeho pozice ve stromu – postupuje se stejně jako při vyhledávání, jako hledaná hodnota se použije klíč vkládaného uzlu. Tato fáze může vést ke dvěma různým výsledkům:

• klíč byl nalezen, strom tedy dotyčnou hodnotu již obsahuje a není třeba ji vkládat (komplikovanější varianty připouštějící vícenásobný výskyt stejného klíče by pokračovaly dál do podstromu připouštějícího rovnost)
• algoritmus narazil na neexistující uzel, nový uzel bude vložen na toto místo, protože sem podle hodnoty svého klíče patří

Zde je typický příklad vkládání do binárního vyhledávacího stromu v jazyce C++:

/* Vkládá se uzel určený ukazatelem "newNode" do podstromu začínajícího uzlem "treeNode" */
void InsertNode(struct node* &treeNode, struct node *newNode)
{
    if (treeNode == NULL)
      treeNode = newNode;
    else if (newNode->value < treeNode->value)
      InsertNode(treeNode->left, newNode);
    else if (newNode->value > treeNode->value)
      InsertNode(treeNode->right, newNode);
}

Popsaná „destruktivní“ verze mění strom na místě. Paměťová náročnost je sice konstantní, ale předchozí verze stromu je přepsána novou. Program lze obměnit, jak ukazuje následující příklad. Nyní lze rekonstruovat všechny předchůdce vloženého uzlu. Každý odkaz na původní kořen zůstává validní, což ze stromu dělá persistentní datovou strukturu.

def binary_tree_insert(node, key, value):
    if node is None:
        return TreeNode(None, key, value, None)
    if key == node.key:
        return TreeNode(node.left, key, value, node.right)
    if key < node.key:
        return TreeNode(binary_tree_insert(node.left, key, value), node.key, node.value, node.right)
    else:
         return TreeNode(node.left, node.key, node.value, binary_tree_insert(node.right, key, value))

Takto změněná část programu průměrně využije Θ(log n) a v nejhorším případě Ω(n) paměti.

V obou verzích zabere tato operace v nejhorším případě čas úměrný výšce stromu, to znamená O(log n) času v průměru přes všechny stromy, ale O(n) času v nejhorším případě.

Jiný způsob jak vysvětlit proces vkládání nového uzlu do stromu je následující. Hodnota nového uzlu je nejdříve srovnávána s hodnotou kořene. Pokud je jeho hodnota menší než hodnota kořene, pak je srovnávána s hodnotou levého potomka kořene. Pokud je hodnota větší, je srovnávána s hodnotou pravého potomka kořene. Tento proces pokračuje, dokud není nový uzel srovnáván s uzlem bez potomka v hledaném směru a pak je v tomto směru nový uzel přidán v závislosti na jeho hodnotě.

Existují i další způsoby vkládání uzlů do binárního stromu, ale toto je jediný způsob vkládání uzlů do listů se současným zálohováním BST struktury.

Zde nastává několik případů ke zvážení.

• Odstranění listu: Odstranění uzlu bez potomků se jednoduše provede odstraněním uzlu ze stromu.
• Odstranění uzlu s jedním potomkem: Provede se nahrazením uzlu uzlem potomka.
• Odstranění uzlu se dvěma potomky: Nechť se odstraněný uzel nazývá N. Pak je hodnota uzlu N nahrazena nejbližší vyšší (nejlevější uzel pravého podstromu), nebo nižší hodnotou (nejpravější uzel levého podstromu). Takový uzel má nanejvýš jednoho potomka, lze jej tedy ze stromu vyjmout podle jednoho z předchozích pravidel. Obě možnosti ilustruje následující obrázek, kdy je ze stromu odstraněn uzel s klíčem 7. V dobré implementaci je doporučeno obě varianty střídat, jinak dochází k narušení rovnováhy.

Mazání uzlu se dvěma potomky

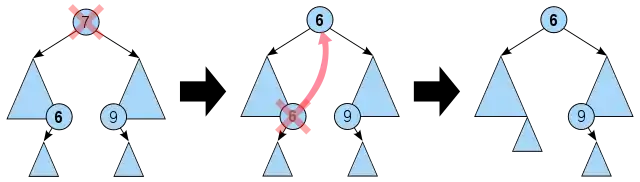
Zde je destruktivní příklad odstranění uzlu v jazyce C++:

void DeleteNode(struct node * & node) {
    if (node->left == NULL) { 
        struct node *temp = node;
        node = node->right;
        delete temp;
    } else if (node->right == NULL) {
        struct node *temp = node;
        node = node->left;
        delete temp;
    } else {
        // Uzel má dva potomky, hledej předchůdce (nejpravější potomek levého podstromu).
        struct node **temp = &node->left; // získej levého potomka mazaného uzlu 

        // najdi nejpravějšího potomka podstromu levého uzlu mazaného uzlu (předchůdce)
        while ((*temp)->right != NULL) {
            temp = &(*temp)->right;
        }

        // zkopíruj hodnotu předchůdce do mazaného uzlu
        node->value = (*temp)->value;

        // nyní smaž předchůdce - jeho hodnota byla přesunuta do původně mazaného uzlu
        DeleteNode(*temp);
    }
}

Přestože tato operace vždy neprochází strom až ke spodním listům, stát se to může, takže v nejhorším případě je spotřebovaný čas úměrný výšce stromu. Nepotřebuje ho více dokonce ani když má uzel dva potomky, protože stále prochází jednu cestu a nenavštěvuje žádný uzel dvakrát.

Průchod binárním vyhledávacím stromem nijak nevyužívá jeho speciální vlastnosti a odpovídá průchodu běžným stromem.

BST může být využit k implementaci jednoduchého, ale neefektivního řadicího algoritmu. Podobně jako v algoritmu heapsort vkládáme všechny hodnoty které chceme seřadit do vhodně uspořádané datové struktury – v tomto případě se jedná o strukturu binárního stromu. Následně stromem projdeme in-order do hloubky a získáme seznam hodnot uspořádaný podle velikosti.

Funkce build_binary_tree spotřebuje v nejhorším případě ${\displaystyle \Theta (n^{2})}$ času, a to pokud se přidávají již seřazené hodnoty. Ty se totiž spojí do seznamu takže strom nemá levé větve. Například build_binary_tree([1, 2, 3, 4, 5]) vytvoří strom (None, 1, (None, 2, (None, 3, (None, 4, (None, 5, None))))).

Existuje několik postupů, jak překonat tyto nedostatky. Nejčastější je samovyvažovací binární strom jehož časová náročnost O(n . log n) je asymptoticky optimální s řazením comparison sort.

V praxi ale špatný výkon vyrovnávací paměti a časová i paměťová režie (obzvlášť pro alokaci uzlů) způsobují, že řazení založené na BST zaostává za ostatními asymptoticky optimálními algoritmy, jako je algoritmus pro řazení rychlé řazení, či řazení haldou pro řazení statických seznamů. Na druhou stranu, je to jedna z nejefektivnějších metod inkrementálního řazení kde přidávání položek do seznamu zachová seznam seřazený.

D. A. Heger v článku [1] porovnal výkonnost jednotlivých variant binárních vyhledávacích stromů. V průměru nejlepšího výkonu dosáhl treap, zatímco výkon červeno-černého stromu nejméně kolísal.

Pokud se neplánují změny vyhledávacího stromu a přesně víme, jak často bude ke každému uzlu přistupováno, lze vytvořit optimální BST, kde je při vyhledávání průměrná doba vyhledání uzlu minimalizována.

Předpokládejme, že známe jednotlivé prvky a pro každý z nich známe průměrný počet jeho hledání. Pomocí dynamického programování pak lze najít optimální řešení.

I v případě, že známe jen odhad ceny vyhledávání, může takový systém v průměru podstatně zrychlit vyhledání. Například pokud máme BST českých slov použitých v korektoru chyb, je možné vyvážit strom podle frekvence použití slov v textu přemístěním slov jako jsou „a“ a „nebo“ blíže ke kořeni a slova jako „chřástal“ k listům. Strom je podobný Huffmanově stromu v tom, že častější uzly jsou blíže kořeni. Nicméně Huffmanovy stromy udržují datové prvky pouze v listech a ty není nutné řadit.

Pokud neznáme pořadí, v němž budou prvky ve stromě navštěvovány, můžeme použít rozvinutý strom, který je asymptoticky stejně dobrý jako statický vyhledávací strom sestavený pro všechny dílčí sekvence vyhledávacích operací.