Splay strom
Splay strom je samovyvažující se binární vyhledávací strom mající tu vlastnost, že prvky, k nimž se nedávno přistupovalo, jsou rychle znovu dostupné. Provádí základní operace jako vkládání, vyhledávání a odstraňování prvků v amortizovaném čase O(log n). Pro mnoho nerovnoměrných posloupností operací pracují splay stromy lépe než ostatní vyhledávací stromy, a to i v případě, že charakteristika posloupnosti není předem známá. Splay strom byl vynalezen Danielem Sleatorem a Robertem Tarjanem.
Všechny obvyklé operace na binárních vyhledávacích stromech jsou spojeny s jednou základní, které se říká splay. Splay uzlu přeuspořádá strom tak, že se daný uzel dostane do kořene. Způsob, jak toho docílit, je provést standardní vyhledávání daného uzlu v binárním stromu a následně provést speciální rotace stromu takové, aby se uzel dostal do kořene.
Výhody a nevýhody
Dobrá výkonnost splay stromu spočívá v tom, že je to strom samovyvažující, a tedy se sám optimalizuje, takže uzly, k nimž se přistupuje často, se dostávají blíže kořeni, kde se k nim dá rychleji dostat. To je výhoda pro většinu praktických aplikací, zejména pro implementaci cache; nicméně při rovnoměrném přístupu je výkon splay stromu podstatně (ne však asymptoticky) horší než jednoduchého nějak vyváženého binárního vyhledávacího stromu.
Splay stromy se také podstatně snadněji implementují než ostatní samovyvažující se binární vyhledávací stromy, jako např. červeno-černý strom nebo AVL-strom, přičemž jejich složitost v průměrném případě je stejná. Splay strom si také nepotřebuje pamatovat žádné pomocné informace, čímž se snižují paměťové nároky. Na druhou stranu uvedené datové struktury garantují složitost v nejhorším případě a mohou být efektivnější při rovnoměrném přístupu.
Příkladem nejhoršího případu u obyčejného algoritmu splay stromu je, když se ke všem prvkům přistupuje postupně v pořadí určeném uspořádáním. To způsobuje, že je strom zcela nevyvážený (vyžaduje to n přístupů, každý z nich má složitost O(log n)). Opakovaný přístup k první položce vyvolá akci, která potřebuje O(n) operací k opětovnému vyvážení stromu před vrácením první položky. To je znatelné zdržení poslední operace, nicméně amortizovaná složitost přes celou posloupnost je stále O(log n). Poslední výzkumy však ukazují, že náhodné vyvažování stromu může tomuto efektu zabránit a dává obdobné výsledky jako ostatní samovyvažující se algoritmy.
Je možné vytvořit perzistentní verzi splay stromu, která umožňuje přistupovat jak k staré, tak k nové verzi po aktualizaci stromu. To vyžaduje amortizovaně O(log n) paměti na jednu aktualizaci.
Na rozdíl od ostatních typů samovyvažujících se stromů splay stromy fungují dobře s uzly obsahujícími identické klíče. I s identickými klíči zůstává amortizovaná složitost O(log n). Všechny operace zachovávají pořadí identických klíčů ve stromě, což je obdobná vlastnost, jakou mají stabilní třídicí algoritmy. Dobře navržená operace vyhledávání může vrátit uzel s daným klíčem nejvíc nalevo nebo nejvíc napravo.
V hašovací tabulce lze použít podobné metody, které posouvají prvek k začátku řetízku nebo k původní hodnotě hašovací funkce a teda se přizpůsobují nerovnoměrnému přístupu. Takto upravená hašovací tabulka umožňuje vyhledání prvku v průměru v O(1) v porovnání s O(log n) u Splay stromů. Hašování také potřebuje (podle implementace) méně nebo žádné režijní pointry a teda je paměťově lepší. Výhoda Splay stromů v tomto kontextu je zaručená amortizovaná složitost a možnost intervalových dotazů.
Operace splay
Když se přistupuje k uzlu x, je na něm vykonána operace splay, která ho přemístí do kořene. Aby se operace vykonala, provede se posloupnost rotací, které uzel x postupně dostávají blíže ke kořeni. Dokud má x prarodiče, jednotlivé kroky závisí na dvou faktorech:
- Jestli x je levým, nebo pravým potomkem svého rodiče p
- Jestli p je levým, nebo pravým potomkem svého rodiče g (prarodiče x).
Z toho vyplývá, že pokud má x prarodiče, mohou nastat čtyři případy, které určují dva typy dvojrotací.
Rotace zig-zag-left
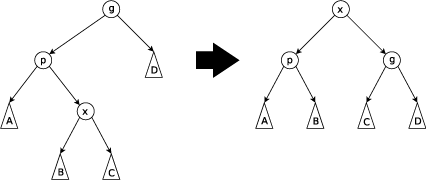
Prvním případem, kdy nastává zig-zag-left rotace[1], je, pokud x je pravým potomkem p a p levým potomkem g (na obrázku). Uzel p se pak stane novým levým potomkem x, g novým pravým potomkem x a podstromy A, B, C a D se přesunou podle potřeby. Druhý případ je zrcadlově otočený, tj., když je x levým potomkem p a p pravým potomkem g. Zig-zag-left dvojrotace je ekvivalentní provedení rotace x a p a následně x a g.
Rotace zig-zig-left
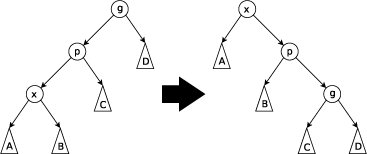
Prvním případem, kdy se provádí rotace zig-zig-left[1], je, když je x levým potomkem p a p je levým potomkem g (na obrázku). Uzel p se stane novým pravým potomkem x, g se stane novým pravým potomkem p a podstromy A, B, C a D se přesunou podle potřeby. Druhý případ zig-zig-left je zrcadlově otočený, tj., pokud x je pravým potomkem p a p je pravým potomkem g.
Rotace zig-left

Třetí typ rotace je, pokud x nemá žádného prapředka. Jedná se o obyčejnou rotaci mezi vrcholem x a p. Tato rotace nastává pouze při posledním kroku, kdy se daný uzel dostává do kořene, v případě, že x je v původním stromu v liché hloubce.
Díky provádění operace splay na požadovaném uzlu se prvky, k nimž se nedávno přistupovalo, drží blízko kořeni a strom zůstává zhruba vyvážený, takže se udržuje požadovaná amortizovaná složitost.