Bernoulliho pokus

Bernoulliho pokus nebo binomický pokus (anglicky Bernoulli trial, binomial trial) je v teorii pravděpodobnosti a statistice náhodný pokus s právě dvěma možnými výsledky, často pojmenovanými „úspěch“ a „neúspěch“, při kterém je pravděpodobnost úspěchu při každém uskutečnění pokusu stejná.[1] Je pojmenovaný po Jacobu Bernoullim, švýcarském matematikovi ze 17. století, který analyzoval tento druh pokusů ve své knize Ars Conjectandi (1713).[2]

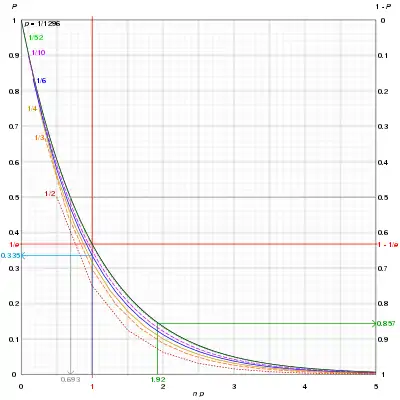
Grafy pravděpodobnosti P, že při provedení n nezávislých pokusů ani jednou nedojde k události, jejíž pravděpodobnost je při každém z pokusů p, pro různé hodnoty p. V grafu jsou vyznačené tři příklady:
Modrá křivka: Při 6 vrzích kostkou je 33,5% pravděpodobnost, že ani jednou nepadne 6 (nebo jiné dané číslo); je vidět, že pravděpodobnost, že ani jednou nedojde k události, která má při jednom pokusu pravděpodobnost 1/n, se zvyšujícím se n rychle konverguje k 0.
Šedá křivka: Aby se dosáhlo šance 50:50 hození Yahtzee (tj. že na 5 šestistranných kostkách padne stejné číslo) vyžaduje 0.69 × 1296 ~ 898 hodů.
Zelená křivka: Stokrát opakované tažení karty (s vracením) z jedné sady bridžových karet bez žolíků (100 = 1.92 × 52) dává 85.7% pravděpodobnost, že alespoň jednou bude taženo zelené eso.

Matematickou formalizaci Bernoulliho pokusu nazýváme Bernoulliho proces. Tento článek obsahuje elementární úvod do konceptu, zatímco článek Bernoulliho proces nabízí pokročilejší informace.

Dva možné výsledky Bernoulliho pokusu lze chápat jako odpověď „ano“ nebo „ne“ na nějakou zjišťovací otázku. Například:

  • Je vrchní karta v zamíchaném balíčku eso?
  • Je novorozené dítě dívka?

Úspěch a neúspěch jsou pouze označení pro dva výsledky, které nesmí být chápány doslovně. Termín „úspěch“ v tomto smyslu pouze znamená, že výsledek splňuje zadanou podmínku, a nemá žádný morální význam. Obecněji, je-li dán jakýkoli pravděpodobnostní prostor, pro jakoukoli událost (množinu výsledků), můžeme definovat Bernoulliho pokus, který odpovídá na otázku, zda k této události došlo nebo ne (událost nebo komplementární událost). K příkladům Bernoulliho pokusů patří:

  • Házení mincí. V tomto kontextu bude panna značit úspěch a orel označuje neúspěch. Spravedlivá mince má pravděpodobnost úspěchu 0,5. V tomto případě existují právě dva možné výsledky.
  • Vrh kostkou, při kterém šestka je „úspěch“ a všechno jiné „neúspěch“. V tomto případě je šest možných výsledků, přičemž jeden z výsledků je událostí „padla šestka“; komplementární událost je „nepadla šestka“, která odpovídá zbylým pěti možným výsledkům.
  • Při provádění průzkumu veřejného mínění výběr náhodného voliče pro zjištění, zda tento volič bude v určitém hlasování hlasovat „ano“.

Definice

Nezávislá opakování pokusů s právě dvěma možnými výsledky se nazývají Bernoulliho pokusy. Nazvěme jeden z výsledků „úspěch“ a druhý výsledek „neúspěch“. Nechť je pravděpodobnost úspěchu v Bernoulliho pokusu a pravděpodobnost neúspěch. Protože jde o komplementární události, je součet těchto pravděpodobností roven jedné: „úspěch“ a „neúspěch“ se vzájemně vylučují a jde o jediné možné výsledky. Platí tedy následující vztahy:

Výsledek Bernoulliho pokusu můžeme vyjádřit také pomocí poměru pravděpodobností (šance): pokud pravděpodobnost úspěchu je p a pravděpodobnost neúspěch q, je poměr pravděpodobností úspěchu poměr pravděpodobností neúspěch . Tyto může také být vyjádřený jako čísla, dělením, což dává šance pro, šance proti, ,

Každá z těchto hodnot je převrácenou hodnotou druhé, čili jejich součin je 1:

Pokud Bernoulliho pokus reprezentuje událost s konečným počtem stejně pravděpodobných výsledků, z nichž S výsledků považujeme za úspěch a F výsledků za neúspěch, je šance úspěchu a šance neúspěchu To dává následující vztahy mezi pravděpodobnostmi a šancemi:

Při tomto výpočtu šancí nedělíme počtem výsledků, ale pravděpodobností, výsledný poměr je však stejný, protože tyto poměry se liší pouze vynásobením obou členů stejnou konstantou.

Hodnoty náhodné proměnné popisující Bernoulliho pokusy se obvykle kódují jako 1 = „úspěch“, 0 = „neúspěch“.

Bernoulliho pokus je úzce spjatý s binomickým pokusem, který sestává z pevného počtu statisticky nezávislých Bernoulliho pokusů, každý s pravděpodobností úspěchu , při nichž počítáme počet úspěchů. Náhodná proměnná odpovídající binomické se označuje a říkáme o ní, že má binomické rozdělení. Pravděpodobnost právě úspěchů v pokusu je

kde je binomický koeficient.

Provádění Bernoulliho pokusů může také vést na negativně binomické rozdělení (které počítá počet úspěchů v řadě opakovaných Bernoulliho pokusů, dokud není pozorován zadaný počet chyb), případně jiná rozdělení.

Pokud se provádí více Bernoulliho pokusů, které mají různé pravděpodobnosti úspěchu mluvíme o Poissonových pokusech.[3]

Příklad: házení mincí

Uvažujme jednoduchý pokus, při němž čtyřikrát hodíme spravedlivou mincí. Najděte pravděpodobnost, že právě dva výsledky jsou panna.

Řešení

Pro tento pokus, nechť panna je definována jako úspěch a orel jako neúspěch. Pokud předpokládáme, že mince je spravedlivá, pravděpodobnost úspěchu je . Pravděpodobnost neúspěchu je tedy

.

Použitím výše uvedené rovnice lze spočítat pravděpodobnost, že ze čtyř vrhů padnou právě dvě panny:

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Bernoulli trial na anglické Wikipedii.

  1. PAPOULIS, A. Probability, Random Variables, and Stochastic Processes. 2. vyd. New York: McGraw-Hill, 1984. S. 57–63. (anglicky)
  2. USPENSKY, James Victor. Introduction to Mathematical Probability. New York: McGraw-Hill, 1937. Dostupné online. S. 45. (anglicky)
  3. MOTWANI, Rajeev; RAGHAVAN, P. Randomized Algorithms [online]. New York: Cambridge University Press, 1995. S. 67–68. (anglicky)

Související články

Externí odkazy
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.