Výtok otvorem

Výtok malým otvorem ve dně nádoby

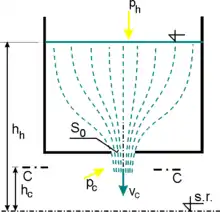
Malý otvor může být ve dně nebo ve stěně nádoby. Uvažujme nejprve malý ostrohranný otvor (provedení ostré hrany viz heslo přeliv) ve středu dna nádoby, resp. v takové vzdálenosti od stěn, že se jejich vliv na proudění již neuplatňuje. Řešení vychází z řešení Bernoulliho rovnice pro hladinu a pro zúžený průřez paprsku (tzv. vena contracta)[1][2]. Je vhodné si uvědomit, jak vlastně proudění v tomto případě vypadá. Voda proudí symetricky ze všech stran k výtokovému utvoru, přičemž se však podstatným způsobem mění zakřivení proudnic (viz obrázek) - proudnice více vzdálené od osy otvoru jsou více zakřiveny, a to zejména na hraně výtokového otvoru. Tím dochází k tomu, že parsek se za výtokovým otvorem zužuje; maximální zúžení je dosaženo poměrně blízko za hranou otvoru (u kruhového otvoru se udává vzdálenost vena contracta ca ${\displaystyle 0,5d}$), takže pro malý otvor v dostatečné hloubce pod hladinou lze tuto vzdálenost zpravidla zanedbat.

Bernoulliho rovnici můžeme napsat ve tvaru

${\displaystyle h_{h}+{p_{h} \over \rho g}+{{\alpha _{0}v_{0}^{2}} \over {2g}}=h_{c}+{p_{c} \over \rho g}+{{\alpha _{c}v_{c}^{2}} \over {2g}}+Z}$

kde ${\displaystyle h}$ [m] je výška nad srovnávací rovinou, ${\displaystyle p}$ [Pa] tlak okolního prostředí, resp. v nádrži nad hladinou, ${\displaystyle \rho }$ [kgm⁻³] hustota kapaliny, ${\displaystyle g}$ [ms⁻²] tíhové zrychlení, ${\displaystyle \alpha }$ [-] Coriolisovo číslo, ${\displaystyle v}$ [ms⁻¹] střední průřezová rychlost kapaliny a ${\displaystyle Z}$ [m] ztrátová výška. Přitom index ${\displaystyle h}$, resp. ${\displaystyle 0}$ odkazuje k hladině v nádobě, zatímco index ${\displaystyle c}$ odkazuje k profilu vena contracta.

Ztrátu energie můžeme vyjádřit (jak je v hydraulice běžné) jako část rychlostní výšky, zde ve vena contracta,

${\displaystyle Z=\zeta {v_{c}^{2} \over {2g}}}$

kde ${\displaystyle \zeta }$ [-] je ztrátový součinitel. Pokud srovnávací rovinu vložíme do profilu vena contracta, můžeme z výše uvedené rovnice po dosazení za ztrátu snadno určit výtokovou rychlost ${\displaystyle v_{c}}$,

${\displaystyle v_{c}={1 \over {\sqrt {\alpha _{c}+\zeta }}}{\sqrt {2g{\Bigl (}h+{{p_{h}-p_{c}} \over {\rho g}}+{{\alpha _{0}v_{0}^{2}} \over {2g}}{\Bigr )}}}}$

kde ${\displaystyle h}$ [m] je výška hladiny v nádrži nad profilem vena contracta (tzv. tlačná výška). Člen rovnice před odmocninou můžeme nazvat rychlostní součinitel výtokové rychlosti a označit jej ${\displaystyle \varphi }$ [-],

${\displaystyle \varphi ={1 \over {\sqrt {\alpha _{c}+\zeta }}}}$.

Protože vzdálenost vena contracta od roviny výtokového otvoru je malá, lze ji zanedbat a potom ${\displaystyle h}$ bude přímo hloubka kapaliny v nádrži. Pokud bude nádrž tzv. velká (poměr plochy výtokového otvoru a plochy hladiny v nádrži je dostatečně malý), můžeme zanedbat rychlostní výšku přítokové rychlosti ${\displaystyle v_{0}}$. A pokud na hladinu v nádrži bude působit atmosférický tlak a paprsek bude vytékat do volného prostoru též s atmosférickým tlakem, bude jejich rozdíl roven nule a rovnice se zjednoduší na tvar

${\displaystyle v_{c}=\varphi {\sqrt {2gh}}}$

což je v podstatě Toricelliho vzorec, odvozený již v 1.polovině 17. stol.

Výše uvedené způsoby výpočtu můžeme použít i pro výtok otvorem ve svislé stěně, pokud za ${\displaystyle h}$ bereme hloubku těžiště plochy otvoru pod hladinou kapaliny.

Pokud potřebujeme stanovit průtok kapaliny ${\displaystyle Q}$ [m³s⁻¹] při výtoku otvorem, vyjdeme z rovnice spojitosti. Je však třeba vzít v úvahu zúžení výtokového paprsku; zaveďme tedy tzv. součinitel zúžení parsku, definovaný vztahem

${\displaystyle \varepsilon ={S \over S_{0}}}$

kde ${\displaystyle S}$ [m²] je plocha výtokového paprsku ve vena contracta a ${\displaystyle S_{0}}$ [m²] je plocha výtokového otvoru. Potom ${\displaystyle S=\varepsilon S_{0}}$ a průtok (v nejjednodušší formě, kdy můžeme zanedbat přítokovou rychlost, nádrž má volnou hladinu a paprsek vytéká do volna) tedy bude

${\displaystyle Q=Sv_{c}=\varepsilon \varphi S_{0}{\sqrt {2gh}}=\mu S_{0}{\sqrt {2gh}}}$

kde ${\displaystyle \mu =\varepsilon \varphi }$ [-] je tzv. výtokový součinitel (součinitel výtoku).

Otvor ve dně můžeme považovat za malý, pokud největší vzdálenost jeho okraje od těžiště je

${\displaystyle \max a_{T}<(0,25-0,3)h}$[1],

otvor ve svislé či šikmé stěně pokud hloubka nejvyššího bodu obvodu otvoru pod hladinou je minimálně ${\displaystyle 10a}$ kde ${\displaystyle a}$ [m] je svislý rozměr otvoru[2].

Nátrubky[2]

Kapacita výtoku otvorem je poměrně malá, dá se však zvětšit, resp. podle speciálních požadavků upravit úpravou hrany otvoru nebo pomocí nátrubku - krátkého kusu potrubí nebo tvarovky (rozšíření, zúžení proudu) nasazené na otvor tak, že hrana otvoru lícuje s povrchem nátrubku (viz obrázek).

Nátrubky: a) vnější válcový; b) vnitřní válcový; c) kónicky zúžený; d) kónicky rozšířený

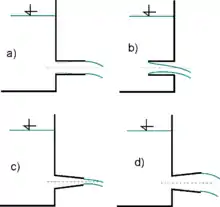
Již prostým zaoblením hrany výtokového otvoru lze získat hodnotu výtokového součinitele až ${\displaystyle \mu =0,74}$. Pokud je vnější válcový nátrubek dostatečně dlouhý (tj. ${\displaystyle L\geq 3d}$ kde ${\displaystyle d}$ [m] je průměr otvoru, resp. nátrubku), paprsek se po zúžení opět rozšíří na celý profil, a tedy bude ${\displaystyle \varepsilon =1}$, ${\displaystyle \mu =\varphi =0,81}$. Přitom ale v místě maximálního zúžení paprsku dojde k vytvoření podtlaku (podrobněji viz literatura).

Vnitřní válcový nátrubek má, pokud je krátký (${\displaystyle L<3d}$) velkou kontrakci a tudíž součinitele ${\displaystyle \mu =0,51}$. Vzhledem k velké kontrakci bude výtokový paprsek při malé délce nátrubku volný (viz obrázek b)), při větší délce paprsek opět vyplní celý profil a výtokový součinitel bude ${\displaystyle \mu =0,71}$.

Plynule zúžený nátrubek by měl co nejlépe sledovat kontrahující paprsek. Optimální je použití Lískovcem odvozeného tvaru (strofoida)[1] kde lze dosáhnout součinitele výtoku až ${\displaystyle \mu =0,987}$. Nevýhodou je dosti složitý tvar; řídící křivku lze nahradit složeným kruhovým obloukem (za cenu nižšího součinitele výtoku).

Kónicky zúžený nátrubek značně omezuje kontrakci paprsku; nejvyšší účinnost má při vrcholovém úhlu ${\displaystyle \delta =12^{\circ }-15^{\circ }}$, kdy výtokový součinitel dosahuje hodnoty ${\displaystyle \mu =0,94}$. Pro větší úhly účinnost značně klesá. Vzhledem k tomu, že tento nátrubek zvětšuje rychlost výtokového paprsku a tím i jeho dosah, používá se jej u proudnic požárních hadic a pro hydromechanizaci.

Kónicky rozšířený nátrubek má díky v něm vznikajícímu podtlaku poměrně značnou kapacitu ve výtokovém otvoru (${\displaystyle \mu =0,85}$); pokud uvažujeme jeho výtokový (nejširší) profil, má malou kapacitu a paprsek z něj vytéká s nejmenší rychlostí - je tedy vhodný tam, kde je žádoucí omezit ztráty kinetické energie (např. savky turbin). Výtokový součinitel ${\displaystyle \mu =0,45-0,50}$ (pro nejširší profil). Vrcholový úhel nesmí být velký (${\displaystyle \max \delta =5^{\circ }-7^{\circ }}$), při větších vrcholových úhlech dochází k odtrhávání proudu od stěn, vzniku vírových oblastí a dalších nestabilit, a dalšímu snižování kapacity zvýšením ztrát.

Výtok velkým otvorem

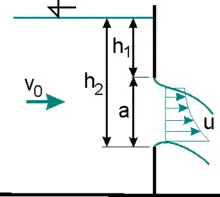
Uvažujme velký (tzn. ${\displaystyle h_{T}<(2-3)a}$ kde ${\displaystyle h_{T}}$ [m] je hloubka těžiště výtokového otvoru pod hladinou a ${\displaystyle a}$ [m] je svislý rozměr otvoru) obdélníkový otvor rozměru ${\displaystyle a.b}$ kde ${\displaystyle b}$ [m] je šířka otvoru, ve svislé stěně. Protože v tomto případě již nelze brát jakousi střední rychlost v otvoru, jelikož výtoková rychlost se významně mění s hloubkou, uvažujme rychlost ${\displaystyle u}$ [ms⁻¹] elementárního proudového vlákna v hloubce ${\displaystyle h}$ pod hladinou. Obdobně výše uvedenému odvození lze ukázat, že tato rychlost

${\displaystyle u=\varphi {\sqrt {2g{\Bigl (}h+{{\alpha _{0}v_{0}^{2}} \over {2g}}{\Bigr )}}}}$.

Proudové vlákno má plochu ${\displaystyle dS=b.dh}$ a tudíž elementární průtok tímto vláknem je

${\displaystyle dQ=dS.u=\varphi \varepsilon b{\sqrt {2g{\Bigl (}{h+{{\alpha _{0}v_{0}^{2}} \over {2g}}}{\Bigr )}}}dh=\varphi \varepsilon b{\sqrt {2g(h+k)}}dh}$

kde ${\displaystyle k}$ [m] je rychlostní výška přítokové rychlosti.

Integrujme tento elementární průtok po ploše otvoru:

${\displaystyle Q=\int _{S}dQ=\mu b{\sqrt {2g}}\int _{h_{1}}^{h_{2}}(h+k)^{1/2}dh={2 \over 3}\mu b{\sqrt {2g}}[(h_{2}+k)^{3/2}-(h_{1}+k)^{3/2}]}$

kde ${\displaystyle h_{2}}$ [m] je hloubka dolní, ${\displaystyle h_{1}}$ [m] hloubka horní hrany výtokového otvoru pod hladinou v nádrži. Výtokový součinitel i přítokovou rychlost uvažujeme globální, pro celý otvor. Pokud je přítoková rychlost dostatečně malá (resp. je dostatečně malá výška přítokové rychlosti), lze člen ${\displaystyle k}$ zanedbat. Obdobným způsobem lze odvodit vztah pro výpočet průtoku i pro otvor jiného tvaru (kruh viz literatura).

Součinitel výtoku literatura udává hodnotou ${\displaystyle \mu =0,65-0,70}$ pro velké otvory se všestranným zúžením a otvory u dna (např. stavidlo na stupni) s podstatným bočním zúžením , ${\displaystyle \mu =0,70}$ pro otvory se všestranným nedokonalým zúžením, ${\displaystyle \mu =0,70-0,75}$ pro otvory u dna s průměrným bočním zúžením a ${\displaystyle \mu =0,80-0,85}$ pro otvory s plynulým bočním zúžením. Přiřazení do jednotlivých kategorií literatura ponechává na ostrovtipu výpočtáře.

a) otvor zcela zatopený; b) otvor částečně zatopený

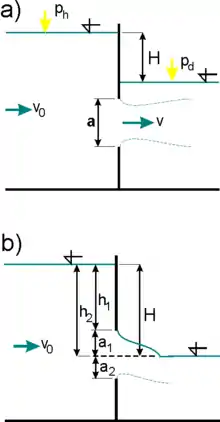
Výpočet průtoku zatopeným otvorem (tj. otvorem, který je celý umístěn pod hladinou spodní vody) je totožný pro malý i velký otvor. Pro velký otvor však rozlišujeme dva různé případy s různým řešením - otvor zcela zatopený, a otvor částečně zatopený, kde hladina dolní vody protíná otvor uvnitř jeho plochy.

Princip výtoku otvorem se prakticky používá např. při měření (hrubšího rázu) průtoku při výtoku např. pod jezovými uzávěry (stavidly, segmenty, ...) a pod. Dvě zajímavé aplikace představuje Mariottova láhev a tzv. danaida.

Mariottova láhev

Mariottova láhev

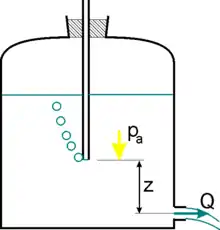
Mariottova láhev je uzavřená nádoba naplněná kapalinou, zpočátku s menším volným prostorem nad hladinou, s výtokovým otvorem (obvykle je opatřen kohoutem) v blízkosti dna. Přes uzávěr je vedena trubice, která končí ve výšce ${\displaystyle z}$ [m] nad těžištěm výtokového otvoru v nádobě (viz obrázek). Je-li Mariottova láhev uvedena v činnost, vznikne nad hladinou podtlak a z trubice začne vybublávat vzduch - to znamená, že v konci trubice, resp. ve výšce konce trubice je atmosférický tlak, takže průtok otvorem bude

${\displaystyle Q=\mu S{\sqrt {2gz}}}$ .

Tento průtok se bude udržovat na konstantní hodnotě až do chvíle, kdy hladina v nádobě poklesne na úroveň dolního konce trubice - pak se již bude průtok se snižováním hladiny v nádobě snižovat též.

Mariottova láhev se běžně využívá pro dávkování menších průtoků kapalin (např. stopovačů při měření průtoku směšovací metodou).

• Výtok otvorem - sylabus přednášky HYA (FSv ČVUT)