Limita funkce
Limita funkce slouží v matematice ke zkoumání chování funkce v okolí určitého bodu. Je to základní pojem v matematické analýze a v diferenciálním a integrálním počtu.
| 1 | 0.841471 |
| 0.1 | 0.998334 |
| 0.01 | 0.999983 |
| 0.001 | 0.999999 |
| 0 | nedefinováno (0/0) |
| -0.001 | 0.999999 |
| -0.01 | 0.999983 |
| -0.1 | 0.998334 |
| -1 | 0.841471 |
Pokud bereme funkci f jako předpis, který hodnotě x přiřazuje funkční hodnotu f(x), pak f má v bodě p limitu L, jestliže pro x v okolí bodu p jsou hodnoty f(x) blízko L. Matematická definice, navržená na začátku 19. století, vyžaduje, aby se pro libovolně malou odchylku od L dalo najít okolí bodu p, že pro každé x v tomto okolí se f(x) liší od L o méně než povolenou odchylku.
Matematicky zapisujeme, že pro x blížící se k p se hodnota f(x) blíží k L výrazem .
Hlavní motivací pro používání limit je možnost „opravit“ chování funkce. Pokud nelze hodnotu funkce v určitém bodě spočítat (např. kvůli dělení nulou), ale v jeho okolí se chová „rozumně“ (viz tabulka s funkcí (sin x)/x vpravo), můžeme funkci opravit tak, že její funkční hodnotu v problematickém bodě nahradíme limitou. Zda se funkce v okolí určitého bodu chová rozumně, lze poznat podle toho, že limita existuje.

Pojem limity má mnoho aplikací v matematické analýze. Například definice spojitosti používají limitu: funkce je spojitá, pokud se její funkční hodnota v každém bodě rovná její limitě v tomto bodě. Limity se proto používají pro funkce, které se chovají „nepěkně“; u „pěkných“ (například spojitých) funkcí je možné pracovat přímo s funkčními hodnotami. Jak snadno můžeme dostat „nepěknou“ funkci ukazuje definice derivace: derivace je limita podílu přírůstku funkce při malé změně x (z x na x+h) dělené změnou x:
Pokud bychom dosadili za h nulu, dostali bychom výraz nula děleno nulou. Pokud použijeme příliš velký přírůstek h, hodnotu derivace nedostaneme přesně. Použitím malých hodnot h dostaneme hodnotu limity s libovolnou přesností.
Limita reálné funkce reálné proměnné
Definice podle Cauchyho
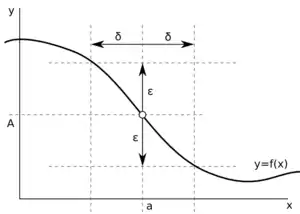
- Říkáme, že reálné číslo je limitou funkce v bodu , jestliže leží v uzávěru a k libovolnému reálnému číslu existuje takové , že pro všechna taková, že ( tedy musí ležet v tzv. prstencovém okolí bodu ) platí .
Tato definice říká, že f(x) má v a limitu A, jestliže f(x) se liší od čísla A velmi málo, je-li x hodně blízko bodu a.
Limitu má smysl zkoumat jen v uzávěru definičního oboru D (bez samotného bodu a); jinými slovy, libovolně blízko k bodu a musí být funkce někde definována. Definice neobsahující tuto podmínku by umožnila tvrdit, že funkce f(x)=x definovaná na intervalu má v bodě 6 limitu -123456 (každé číslo by bylo limitou v každém bodě, který není "nekonečně blízko" k definičnímu oboru).
Definice podle Heineho
Hlavní myšlenka je problém limity funkce převést na již známý problém limity posloupnosti.
- Nechť je hromadným bodem D(f) (v každém jeho prstencovém okolí leží alespoň jeden bod D(f)). Číslo A nazveme limita funkce f v bodě právě tehdy, když pro každou posloupnost platí .
- Značíme
Heineho a Cauchyova definice jsou ekvivalentní. Heineho se používá k výpočtu limit, Cauchyova častěji k důkazům.
Pokud je limita počítána v definované části funkce, jedná se o funkční hodnotu tohoto místa, právě když je v tom místě funkce spojitá.
Limita v nekonečnu a nevlastní limita
Pomocí rozšířených reálných čísel lze definovat limitu i v případě, že a nebo A je kladné nebo záporné nekonečno.
Pro rozlišujeme 4 případy, vlastní limita v vlastním bodě, nevlastní limita v vlastním bodě, vlastní limita v nevlastním bodě a nevlastní limita v nevlastním bodě. Pro vlastní limity platí, že , pro nevlastní potom nebo . Pro limity ve vlastním bodě platí , pro limity v nevlastním bodě potom nebo
Příklad vlastní limity v vlastním bodě ( )
Příklad nevlastní limity v vlastním bodě ( )
Příklad vlastní limity v nevlastním bodě ( )
Příklad nevlastní limity v nevlastním bodě ( )
Limita funkce více proměnných
O funkci n-proměnných říkáme, že má v bodě limitu K, pokud ke každému (libovolně malému) číslu existuje takové číslo , jež je v obecném případě závislé na volbě , že pro všechny body z -okolí bodu A s výjimkou samotného bodu A platí . Takovou limitu značíme některým z následujících způsobů.
Limita funkce n proměnných je tedy definována obdobným způsobem jako limita funkce jedné proměnné.
U funkce n proměnných je možné provádět limitní přechod nejen vůči všem proměnným, tzn. , ale také vzhledem několika nebo jen jedné z proměnných, tzn. např. . Tedy např.
- ,
kde g je funkcí proměnných.
Limita komplexní funkce
O komplexní funkci definované v okolí bodu říkáme, že má v limitu , jestliže k libovolnému existuje -okolí bodu takové, že
Limitu v bodě zapisujeme
- .
Formálně je tedy zápis stejný jako v případě reálných funkcí.
Limita může být komplexním číslem.
Limita zprava a zleva
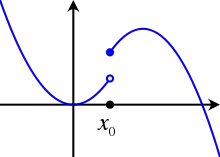
O funkci říkáme, že má v bodě limitu zprava, resp. zleva, pokud k libovolnému číslu existuje takové číslo , jehož hodnota může v obecném případě záviset na volbě , že pro všechna x z pravého resp. levého okolí bodu , z něhož vyjmeme bod , tedy pro všechna x splňující podmínku , resp. , platí , což zapisujeme
- - označována jako limita zprava
- - označována jako limita zleva
Funkce má v bodě a limitu právě tehdy, pokud má v tomto bodě současně limitu zleva i zprava a tyto limity se rovnají.

Funkce nemá v bodě 0 limitu, ačkoliv má obě jednostranné limity
Vlastní a nevlastní limita
Limitu nazýváme vlastní nebo konečnou limitou funkce v bodě a, je-li konečné číslo.
Limitu funkce v daném bodě a označíme jako nevlastní , resp. , pokud k libovolně velkému číslu existuje takové , že pro všechna x z -okolí bodu a s výjimkou bodu a samotného platí , resp. , tedy
Nevlastní limitu lze definovat také zprava nebo zleva, bereme-li pouze pravé nebo levé okolí bodu a.
Limita v nevlastních bodech
Limitu funkce lze počítat ve vlastních i nevlastních bodech, přičemž vlastním bodem je myšleno libovolné reálné číslo, nevlastním pak či .
Říkáme, že funkce má vlastní limitu v nevlastním bodě resp. právě tehdy když:
resp. .
Také v nevlastním bodě může být limita nevlastní, tzn. .
Vlastnosti
- Mějme libovolné číslo c, funkci , která má v bodě a limitu A a funkci , která má ve stejném bodě limitu B, pak platí následující vztahy
- , pokud
- Mějme funkci , která má v bodě a limitu A, tzn. , a funkci , která má v bodě A limitu B, tedy . Pokud existuje takové , že pro všechna x splňující podmínku platí , pak
- Máme-li dvě funkce , pro něž v okolí nějakého bodu a platí , pak v případě, že obě funkce mají v bodě a limitu, bude platit
- Pokud v okolí bodu a platí a existují limity a , pak existuje také limita , a její hodnota je (tzv. věta o třech limitách, známá spíše jako věta o dvou policajtech).
Příklad funkce bez limity
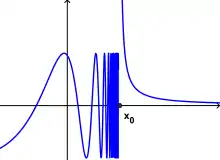
Funkce
nemá limitu v bodě .
Související články
Externí odkazy
 Obrázky, zvuky či videa k tématu Limita funkce na Wikimedia Commons
Obrázky, zvuky či videa k tématu Limita funkce na Wikimedia Commons