Lifting

Lifting je výpočetní schéma diskrétní vlnkové transformace (DWT). Toto schéma je obvykle rychlejší než naivní výpočet pomocí konvoluce se dvěma zrcadlovými filtry. Tento algoritmus poprvé předvedl Wim Sweldens.

Blokové schéma schématu lifting.

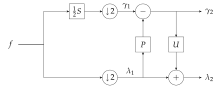
Jakákoli DWT s konečnými filtry může být faktorizována (např. pomocí Eukleidova algoritmu) do posloupností ${\displaystyle N}$ párů predikčních ${\displaystyle P_{n}}$ a aktualizačních ${\displaystyle U_{n}}$ konvolučních operátorů. Každý predikční operátor ${\displaystyle P_{n}}$ odpovídá filtru ${\displaystyle p_{i}^{(n)}}$ a každý aktualizační operátor ${\displaystyle U_{n}}$ filtru ${\displaystyle u_{i}^{(n)}}$.

${\displaystyle P_{n}(z)=\sum _{i}p_{i}^{(n)}z^{-i}}$

${\displaystyle U_{n}(z)=\sum _{i}u_{i}^{(n)}z^{-i}}$

Tato faktorizace není unikátní. Pro symetrické filtry může být tato neunikátnost využita k udržení symetrie kroků liftingu.

Prvním krokem při výpočtu liftingu je rozdělení signálu na sudé a liché vzorky (${\displaystyle s^{(0)},d^{(0)}}$). Následuje sekvence predikcí a aktualizací pomocí výše definovaných operátorů. Predikce ${\displaystyle P_{n}}$ v kroku ${\displaystyle n}$ se počítá nad vzorky ${\displaystyle s^{(n)}}$ a její výsledek se odečte od ${\displaystyle d^{(n)}}$, čímž vzniká ${\displaystyle d^{(n+1)}}$. Následná aktualizace ${\displaystyle U_{n}}$ s počítá nad upravenými ${\displaystyle d^{(n+1)}}$ a přičte se k ${\displaystyle s^{(n)}}$, čímž vzniká ${\displaystyle s^{(n+1)}}$. Výsledkem jsou prokládané koeficienty podpásem L (odpovídá ${\displaystyle s^{(n)}}$) a H (odpovídá ${\displaystyle d^{(n)}}$) diskrétní vlnkové transformace.