Konvexní obal
Podobně jako je lineární obal definován pro lineární kombinace jisté množiny vektorů, lze ve vektorových prostorech definovat i obaly vektorů ve vztahu ke konvexním kombinacím.
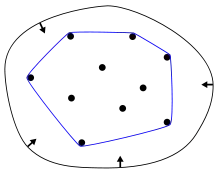
Konvexní obal množiny vektorů v rovině. Můžeme si představit, že okraj obalu je určený gumičkou nataženou kolem vektorů.
Definice
Mějme vektorový prostor nad tělesem a množinu vektorů z . Množinu všech konvexních kombinací této sady vektorů nazýváme konvexní obal vektorů (angl. convex span, convex hull či convex envelope). Někdy se konvexní obal zmíněných vektorů značí jako . V matematické symbolice tedy
kde .
Vlastnosti
Mějme vektorový prostor nad tělesem . Pro konvexní obaly vektorů z lze odvodit mimo jiné následující vlastnosti ().
- Konvexní obal daných vektorů obsahuje i tyto vektory samotné. Neboli
- Důkaz: Doplnit...
- Konvexní obal je skutečně konvexní množina.
- Důkaz: Doplnit...
- Konvexní obal daných vektorů je nejmenší konvexní podmnožina vektorového prostoru obsahující tyto vektory, tj.
- Důkaz: Doplnit...
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.