Eulerova přímka
[[Soubor:EulerGeradeColor.png|náhled|
- e – Eulerova přímka
- H – průsečík výšek
- S – těžiště
- U – střed opsané kružnice]]
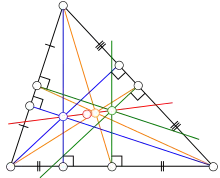
Eulerova přímka, výšky, těžnice, osy stran
Eulerova přímka je přímka nacházející se v každém nerovnostranném trojúhelníku. Tato přímka prochází průsečíkem jeho výšek (ortocentrum), těžištěm a středem opsané kružnice. Těžiště dělí spojnici průsečíku výšek (tj. ortocentra) a středu kružnice opsané v poměru 2:1. Na Eulerově přímce leží také střed kružnice devíti bodů, který je stejnolehlým obrazem středu kružnice opsané se středem stejnolehlosti v těžišti trojúhelníka a koeficientem κ = – 0,5. Rovnostranný trojúhelník Eulerovu přímku nemá, protože v něm všechny tyto čtyři body splývají. V rovnoramenném trojúhelníku je Eulerova přímka kolmá na základnu.
Eulerova přímka je pojmenována po švýcarském matematikovi Leonhardu Eulerovi (1707-1783).
Související články
Externí odkazy
 Obrázky, zvuky či videa k tématu Eulerova přímka na Wikimedia Commons
Obrázky, zvuky či videa k tématu Eulerova přímka na Wikimedia Commons - Zvláštní přímky a kružnice trojúhelníku: http://www.walter-fendt.de/…
- Jiří Šrubař, Vlastnosti trojúhelníka a jejich analogie pro čtyřstěn: http://mat.fsv.cvut.cz/…/srubar.pdf (pdf)
- Mathworld, Euler Line: http://mathworld.wolfram.com/EulerLine.html
Literatura
- ŠVRČEK, Jaroslav; VANŽURA, Jiří. Geometrie trojúhelníka. Praha: Nakladatelství technické literatury, 1988.
Portály: Matematika
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.