Bilineární interpolace

V matematice je bilineární interpolace rozšíření lineární interpolace pro interpolaci funkce dvou proměnných na pravidelnou prostorovou mřížku. Klíčová myšlenka je provést lineární interpolaci nejprve v jednom směru a pak i ve druhém směru.

Čtyři červené tečky ukazují datové body a zelená tečka je bod který chceme interpolovat.

Například bilineární interpolace na jednotkovém čtverci se z-hodnotami 0, 1, 1 a 0.5 jako signalizace. Interpolační hodnoty uprostřed jsou reprezentovány barvami.

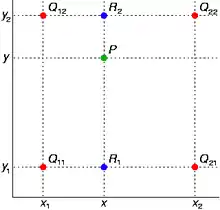
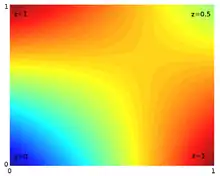
Předpokládejme, že chceme najít hodnotu neznámé funkce f v bodě P = (x, y). Předpokladem je, že známe hodnotu f ve čtyřech bodech Q₁₁ = (x₁, y₁), Q₁₂ = (x₁, y₂), Q₂₁ = (x₂, y₁), a Q₂₂ = (x₂, y₂).

Nejprve provedeme lineární interpolaci v x-ovém směru. To znamená:

${\displaystyle f(R_{1})\approx {\frac {x_{2}-x}{x_{2}-x_{1}}}f(Q_{11})+{\frac {x-x_{1}}{x_{2}-x_{1}}}f(Q_{21})\quad {\mbox{kde}}\quad R_{1}=(x,y_{1}),}$

${\displaystyle f(R_{2})\approx {\frac {x_{2}-x}{x_{2}-x_{1}}}f(Q_{12})+{\frac {x-x_{1}}{x_{2}-x_{1}}}f(Q_{22})\quad {\mbox{kde}}\quad R_{2}=(x,y_{2}).}$

A teď budeme pokračovat v y-ovém směru.

${\displaystyle f(P)\approx {\frac {y_{2}-y}{y_{2}-y_{1}}}f(R_{1})+{\frac {y-y_{1}}{y_{2}-y_{1}}}f(R_{2}).}$

Nyní máme požadovaný odhad f(x, y).

${\displaystyle {\begin{aligned}f(x,y)&\approx {\frac {f(Q_{11})}{(x_{2}-x_{1})(y_{2}-y_{1})}}(x_{2}-x)(y_{2}-y)\\&+{\frac {f(Q_{21})}{(x_{2}-x_{1})(y_{2}-y_{1})}}(x-x_{1})(y_{2}-y)\\&+{\frac {f(Q_{12})}{(x_{2}-x_{1})(y_{2}-y_{1})}}(x_{2}-x)(y-y_{1})\\&+{\frac {f(Q_{22})}{(x_{2}-x_{1})(y_{2}-y_{1})}}(x-x_{1})(y-y_{1}).\end{aligned}}}$

Pokud si vybereme souřadící systém se čtyřmi body, kde funkce f je zadána body (0, 0), (0, 1), (1, 0), a (1, 1), pak se vzorec zjednoduší:

${\displaystyle f(x,y)\approx f(0,0)\,(1-x)(1-y)+f(1,0)\,x(1-y)+f(0,1)\,(1-x)y+f(1,1)xy.}$

Nebo ekvivalentně, maticovými operacemi:

${\displaystyle f(x,y)\approx {\begin{bmatrix}1-x&x\end{bmatrix}}{\begin{bmatrix}f(0,0)&f(0,1)\\f(1,0)&f(1,1)\end{bmatrix}}{\begin{bmatrix}1-y\\y\end{bmatrix}}}$

Oproti tomu, co říká název, interpolace není lineární. Místo toho je její vzorec

${\displaystyle (a_{1}x+a_{2})(a_{3}y+a_{4}),\,}$

takže je součinem dvou lineárních funkcí. Stejně tak lze interpolaci zapsat jako

${\displaystyle b_{1}+b_{2}x+b_{3}y+b_{4}xy\,}$

kde

${\displaystyle b_{1}=f(0,0)\,}$

${\displaystyle b_{2}=f(1,0)-f(0,0)\,}$

${\displaystyle b_{3}=f(0,1)-f(0,0)\,}$

${\displaystyle b_{4}=f(0,0)-f(1,0)-f(0,1)+f(1,1)\,}$.

V obou případech počet konstant (čtyři) odpovídá počtu daných bodů, které funkce f udává. Interpolace je lineární podle přímky, která je rovnoběžná buď se směrem ${\displaystyle x}$ nebo ${\displaystyle y}$, ekvivalentně je-li ${\displaystyle x}$ nebo ${\displaystyle y}$ nastaveno konstantně. Rovnoběžně s další přímkou je interpolace kvadratická.

Výsledek bilineární interpolace je nezávislý na pořadí interpolací. Kdybychom nejprve provedli lineární interpolaci na ose y a pak v x-ovém směru, výsledná aproximace bude stejná.

Zřejmým rozšířením bilineární interpolace je trojrozměrná interpolace – trilineární interpolace.