Bezškálová síť

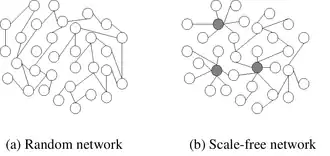
Předepsaná distribuce stupňů vrcholů velmi ovlivňuje celkovou topologii grafu. Nejzajímavější vlastností bezškálových sítí je relativní běžnost vrcholů, jejichž stupeň vysoce převyšuje průměr. Vrcholy s nejvyššími stupni se často nazývají „huby“ ([hʌb]IPA). Tyto huby jsou obklopeny vrcholy s nižšími stupni a ty vrcholy s ještě nižšími atd…

Topologie bezškálových sítí je velmi odolná vůči náhodnému (při rovnoměrném rozdělení pravděpodobnosti) odstranění některých vrcholů. Pravděpodobnost, že hub bude odstraněn je téměř zanedbatelná, protože hubů je málo. Pokud přesto je některý odstraněn, s velkou pravděpodobností graf zůstane souvislý. Na druhou stranu, pokud cíleně odstraníme několik hlavních hubů, graf se rozpadne na několik izolovaných grafů. Huby jsou tedy jak silnou stránkou, tak Achillovou patou bezškálových sítí.

Další důležitou vlastností bezškálových sítí je vytváření shluků, klastrů. Vrcholy s nízkými stupni bývají připojeny k velmi hustým podgrafům a ty bývají s jinými takovými podgrafy spojeny přes huby s ještě vyšším stupněm.

Významnou vlastností bezškálových sítí s ${\displaystyle 2<\gamma <3}$ je jejich velmi malý průměr grafu ${\displaystyle d}$, který s počtem vrcholů ${\displaystyle n}$ roste jen jako ${\displaystyle d\sim \ln \ln n}$. Díky tomu se dá průměr rostoucích bezškálových sítí považovat za téměř neměnný.[2]

Bezškálová síť odpovídá mnoha sítím v reálném světě, v biologii, epidemiologii, sociologii nebo informatice.[1] Jejich koeficient ${\displaystyle \gamma }$ se většinou pohybuje mezi 2 a 3, ale může být i menší než 2.[3] Reálně však většinou nejsou úplně bezškálové.[4]

• Sítě „malého světa“ Proč mají odlišné sítě podobnou strukturu? Miroslav Kotrla, František Slanina Publikováno: Vesmír 80, 611, 2001/11

V tomto článku byl použit překlad textu z článku Scale-free network na anglické Wikipedii.