Antisymetrická relace
Antisymetrická relace je matematický pojem označující relaci, ve které nenastává situace, že by a bylo v relaci s b a zároveň b v relaci s a. Podle toho, jestli se tato podmínka vztahuje i na stejné a, b, se liší pojem slabé a silné antisymetrie.
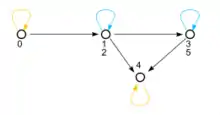
Typy
Slabě antisymetrická relace
Binární relace R na množině X se nazývá slabě antisymetrická, platí-li pro všechna a a b z X, že jestliže a je v relaci s b a b je v relaci s a, pak a = b.
Formálně zapsáno:
„Je menší nebo rovno“ je slabě antisymetrická relace: jelikož je nemožné pro různá a , je slabá antisymetrie zřejmá.
Slabá antisymetrie není opakem symetrie . Existují relace, které jsou jak symetrické, tak slabě antisymetrické (rovnost), existují i relace, které nejsou ani symetrické, ani slabě antisymetrické (dělitelnost v okruhu celých čísel), existují relace, které jsou symetrické, ale nejsou slabě antisymetrické (dělení modulo p, kde p je prvočíslo), a existují relace, které nejsou symetrické, ale jsou slabě antisymetrické („je menší nebo rovno“).
Slabě antisymetrická relace, která je zároveň tranzitivní a reflexivní se nazývá neostré uspořádání (nebo jen uspořádání).
Silně antisymetrická relace
Binární relace R na množině X nazývá silně antisymetrická, platí-li pro všechna a a b z X, že jestliže a je v relaci s b pak b není v relaci s a.
Formálně zapsáno:
Tato podmínka vylučuje existenci prvku a, který by byl v relaci sám se sebou — každá silně antisymetrická relace je proto ireflexivní.
Silně antisymetrická relace je například ostrá nerovnost < na přirozených číslech. To je také příklad ostrého uspořádání — relace, která je silně antisymetrická (z toho ireflexivní) a tranzitivní.
Související články
Literatura
- BALCAR, Bohuslav; ŠTĚPÁNEK, Petr. Teorie množin. 2. vyd. Praha: Academia, 2001. 464 s. ISBN 80-200-0470-X.