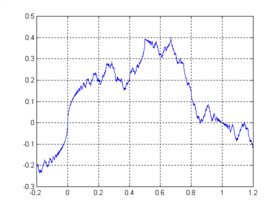
Weierstrassova funkce
Weierstrassova funkce, pojmenovaná po německém matematikovi Karlu Weierstrassovi, je matematická funkce, která je ve všech bodech spojitá, ale v žádném bodě nemá derivaci (není nikde hladká).
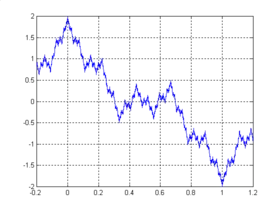
Weierstrassova funkce s konstantami ;

Ukázka soběpodobnosti
Funkce se chová jako fraktál, neboť zvětšené části grafu a původní graf jsou podobné.[1]
Definice
Weierstrassova funkce bývá uváděna v různých tvarech s různými konstantami.
- Podle původní publikace (http://historical.library.cornell.edu/…), en:Weierstrass function a http://planetmath.org/… Archivováno 12. 3. 2007 na Wayback Machine:
- kde , je kladné liché číslo a konstanty splňují následující podmínku.
- Později bylo dokázáno, že poslední uvedenou podmínku lze nahradit podmínkou .
- přičemž údajně podle původní publikace . Tato funkce má však v určitých izolovaných bodech konečné derivace. Podle jiných zdrojů[2] je tato funkce nazývána Riemannova, neboť podle Weierstrasse ji Bernhard Riemann uváděl na svých přednáškách okolo roku 1861.
Související články
Externí odkazy
 Obrázky, zvuky či videa k tématu Weierstrassova funkce na Wikimedia Commons
Obrázky, zvuky či videa k tématu Weierstrassova funkce na Wikimedia Commons
Reference
Portály: Matematika
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.