Vogelova metoda
Vogelova metoda slouží ke geometrickému vyšetření průjezdu kolejového vozidla obloukem. Výsledkem je informace, zda při daném geometrickém uspořádání vozidla a koleje je vůbec možné vozidlo do koleje umístit, či nikoliv. K vyšetření skutečné polohy vozidla na základě silových poměrů potom slouží Heumannova metoda a metody z ní odvozené.
Předpoklady použití
Při použití Vogelovy metody dochází k určitému zjednodušení situace kolejového vozidla v oblouku.
Jednotlivá dvojkolí vozidla jsou znázorněna pouhými body. Přitom je zanedbán fakt, že styk okolku s kolejnicí se nenachází vždy v průmětu osy dvojkolí do vodorovné roviny (zpravidla poněkud předbíhá) a rozchod dvojkolí není znázorněn.
Kolej je znázorněna podobně zjednodušeným způsobem. Namísto rozchodu koleje je znázorněna pouze šířka kolejového kanálu, tj. rozdíl rozchodu koleje a dvojkolí, neboli příčná vůle dvojkolí v koleji.
Měřítka obou os jsou obvykle pro větší názornost rozdílná. V podélném směru se používají měřítka 1:100 nebo 1:50, v příčném 1:1 nebo 1:2. Kruhový oblouk je tak deformován na elipsu. V dřívějších dobách bývaly pro konstrukci těchto elips používány souřadnicové tabulky, dnes je s použitím výpočetní techniky postup značně jednodušší.
Postup řešení
Oblouk bez rozšíření rozchodu
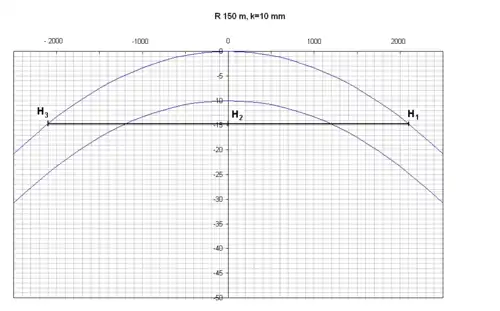
Na následujícím obrázku je znázorněno vyšetření polohy podvozku lokomotivy ř. 781 v oblouku o poloměru 150 m bez rozšíření rozchodu. Tomu odpovídá šířka kolejového kanálu 10 mm (rozdíl rozchodu koleje 1435 mm a dvojkolí 1426 mm v obvykle používaném zaokrouhlení vlivem odlišných poloh měřících bodů koleje a dvojkolí). Osa X je v měřítku 1:50, osa Y 1:1. Je zjevné, že ani v tětivové poloze by se podvozek bez dalších opatření do tohoto oblouku „nevešel“. Zeslabení okolku o obvyklých 15 mm u prostřední nápravy umožní vtěsnání podvozku do koleje, avšak třetí dvojkolí bude nabíhat na vnitřní kolejnici pod poměrně velkým úhlem, což povede ke značnému opotřebení kol i kolejnic.
Oblouk s rozšířeným rozchodem
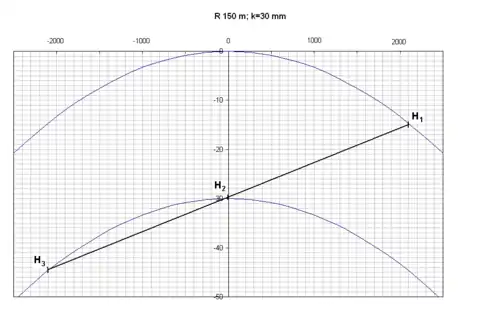
Na druhém obrázku je tatáž situace, avšak v oblouku s rozchodem rozšířeným na 1455 mm. V tomto případě teoreticky dojde k dolehnutí 2. i 3. dvojkolí na vnitřní kolejnici. Pokud budou na prostředním dvojkolí okolky zeslabeny, nebude hrozit vznik příčné řídící síly na druhém dvojkolí.
Příklad použití u lokomotivy řady E 465.0
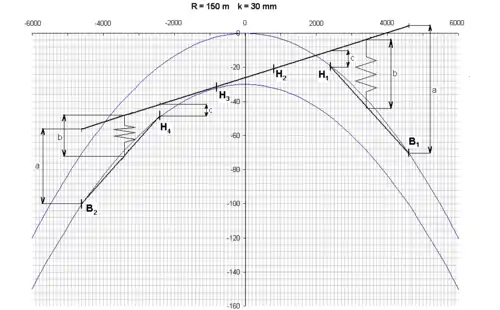
Na obrázku je zobrazeno vyšetření polohy pojezdu lokomotivy ČSD řady E 465.0 v oblouku o poloměru 150 m při šířce kolejového kanálu 30 mm (rozchod koleje rozšířený o 20 mm). Osa y je znázorněna 1:1, osa x v měřítku 1:50. Lokomotiva je opatřena rámovým pojezdem se dvěma Krauss-Helmoltzovými podvozky.
Lze předpokládat, že první dvojkolí dolehne na vnější kolejnici. Stejně tak i první hnací dvojkolí dolehne na vnější kolejnici, neboť je směrováno rámem lokomotivy ven z oblouku. Tím je dána poloha předního Krauss-Helmholtzova podvozku. Poloha rámu lokomotivy vychází z předpokladu maximální příčné vůle otočného čepu Krauss-Helmholtzova podvozku b – jelikož nebyla tato hodnota k dispozici, byla stanovena odhadem podle jiných lokomotiv na 40 mm. Příčný posuv běžné nápravy a = 95 mm, hnacích náprav H1 a H4 c = 20 mm. Zakreslená poloha rámu také odpovídá Heumannově teorii – dvojkolí H2 zaujímá polohu co nejblíže vnější kolejnici, zatímco H3 se blíží spíše radiální poloze a je předpoklad dolehnutí na vnitřní kolejnici. Náprava H4 vedena rámem směřuje při svém pohybu dovnitř oblouku, nabíhá tedy na vnitřní kolejnici a stejně tak i zadní běžné dvojkolí.
Po zakreslení je třeba překontrolovat všechny vůle, zda nebyly při konstrukci grafického zobrazení překročeny.
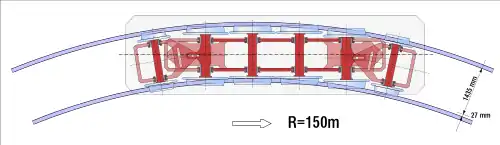
Ve skutečnosti pak vypadá poloha pojezdu přibližně takto:
Literatura
Vogel R.: Zeichnerische Untersuchungen der Bogenbeweglichkeit von Eisenbahnfahrzeugen. Organ für den Fortschritt des Eisenbahnwesens 81 (1926), sešit 17, str. 354-358
Nejepsa,R: Kolejové vozy, část II. – Vozidlo a kolej, SNTL Praha 1956