Varignonova věta
Varignonova věta je v euklidovské geometrii věta, která se zabývá konstrukcí konkrétního rovnoběžníku, varignonského rovnoběžníku, z libovolného čtyřúhelníku (čtyřúhelníku). Věta je pojmenována po Pierru Varignonovi, který ji publikoval v roce 1731.
Věta
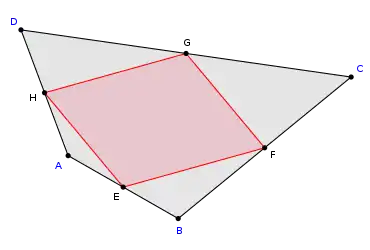
Středy stran libovolného čtyřúhelníku tvoří rovnoběžník. Je-li čtyřúhelník konvexní nebo konkávní (ne komplexní), pak plocha rovnoběžníku je polovinou plochy čtyřúhelníku.
| konvexní čtyřúhelník | konkávní čtyřúhelník | překřížený čtyřúhelník |
|---|---|---|
 |
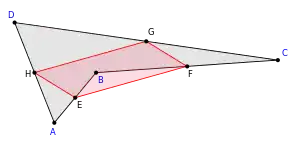 |
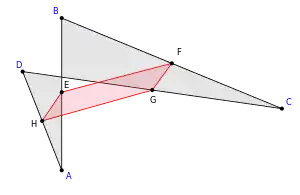 |
Varignonův rovnoběžník
Vlastnosti
Rovinný Varignonův rovnoběžník má také následující vlastnosti:
- Každá dvojice protilehlých stran Varignonova rovnoběžníku je rovnoběžná s úhlopříčkou v původním čtyřúhelníku.
- Strana Varignonova rovnoběžníku je poloviční, pokud je úhlopříčka v původním čtyřúhelníku rovnoběžná.
- Obsah Varignonova rovnoběžníku se rovná polovině obsahu původního čtyřúhelníku. Toto platí pro konvexní, konkávní a překřížené čtyřúhelníky za předpokladu, že tato oblast je definována jako rozdíl obsahů dvou trojúhelníků, ze kterých se skládá. [1]
- Obvod Varignonova rovnoběžníku se rovná součtu úhlopříček původního čtyřúhelníku.
- Úhlopříčky Varignonova rovnoběžníku jsou střední příčky původního čtyřúhelníku.
Délka střední příčky, která v konvexním čtyřúhelníku se stranami a, b, c a d spojuje středy stran a a c, je
- ,
kde p a q jsou délky úhlopříček.[2] Délka střední příčky, která spojuje středy stran b a d, je
[3] :s.p.126
- .
Délka bimediánů (středních příček) může být také vyjádřena dvěma protilehlými stranami a vzdáleností x mezi středy úhlopříček. To je možné při použití Eulerova čtyřúhelníkového teorému ve výše uvedených vzorcích; odkud
a
V konvexním čtyřúhelníku je následující spojení mezi středními příčkami a úhlopříčkami:
- Dvě střední příčky mají stejnou délku, pokud a jen tehdy, jsou-li dvě úhlopříčky kolmé.
- Dvě střední příčky jsou kolmé, pokud a pouze pokud mají dvě úhlopříčky stejnou délku.
Speciální případy
Varignonův rovnoběžník je kosočtverec jestliže dvě úhlopříčky čtyřúhelníku mají stejnou délku, tj. čtyřúhelník je equidiagonální.
Varignonův rovnoběžník je obdélník jestliže úhlopříčky čtyřúhelníku jsou kolmé, tj. čtyřúhelník je orthodiagonální.
Odkazy
Reference
V tomto článku byl použit překlad textu z článku Varignon's theorem na anglické Wikipedii.
- Coxeter, H. S. M. and Greitzer, S. L. "Quadrangle; Varignon's theorem" §3.1 in Geometry Revisited.
- Mateescu Constantin, Answer to Inequality Of Diagonal
- Altshiller-Court, Nathan, College Geometry, Dover Publ., 2007.
Externí odkazy
 Obrázky, zvuky či videa k tématu Varignonova věta na Wikimedia Commons
Obrázky, zvuky či videa k tématu Varignonova věta na Wikimedia Commons
- Varignonova věta v encyklopedii MathWorld (anglicky)
- Varignon Parallelogram in Compendium Geometry
- A generalization of Varignon's theorem to 2n-gons and to 3D at Dynamic Geometry Sketches, interactive dynamic geometry sketches.
- Varignon parallelogram at cut-the-knot-org