Konvexní mnohoúhelník

V geometrii je konvexní mnohoúhelník takový mnohoúhelník, jehož všechny vnitřní úhly jsou konvexní, tedy velikostně menší nebo rovny úhlu přímému (180 stupňů).

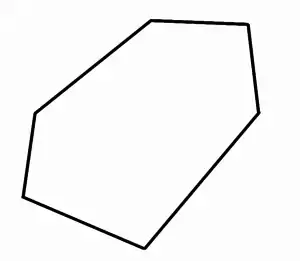
Příklad konvexního mnohoúhelníku
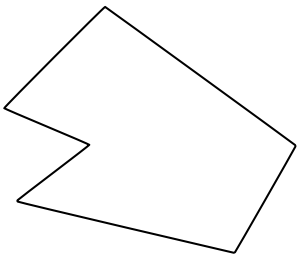
Příklad nekonvexního mnohoúhelníku
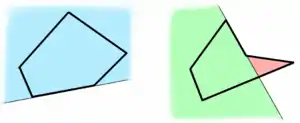
Ke všem stranám konvexního mnohoúhelníku (vlevo) lze přiřadit opěrnou polorovinu, což u nekonvexního (vpravo) nelze.

Vlastnosti
  • Všechny úsečky, jejichž krajní body leží uvnitř konvexního mnohoúhelníku, mají s tímto mnohoúhelníkem všechny své body společné.
  • Každá polorovina, v níž konvexní mnohoúhelník leží, a jejíž hraniční přímka má s mnohoúhelníkem společnou právě jednu jeho stranu, se nazývá opěrná. Konvexní mnohoúhelník je průnikem všech svých opěrných polorovin.
  • Vnitřní úhel konvexního mnohoúhelníku je průnikem opěrných polorovin příslušných dvěma sousedním stranám. Součet velikostí vnitřních úhlů n-úhelníku je roven „ “.
  • Úsečka spojující dva nesousední vrcholy se nazývá úhlopříčka. Počet úhlopříček konvexního mnohoúhelníku je právě „ “.
  • Mnohoúhelník, jemuž lze opsat kružnici, je konvexní, a nazývá se tětivový. Pokud mu lze kružnici vepsat, nazývá se tečnový.

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Convex polygon na anglické Wikipedii.

Literatura
  • POMYKALOVÁ, Eva. Planimetrie. 5. vyd. Praha: Prometheus, 2015. 208 s. ISBN 978-80-7196-358-5. Kapitola Geometrické útvary v rovině, s. 42, 43, 49.

Související články

Externí odkazy
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.