Studentovo rozdělení

Studentovo rozdělení vymyslel anglický statistik William Sealy Gosset publikující pod pseudonymem Student.

Studentovo rozdělení o ${\displaystyle n}$ stupních volnosti, které označujeme ${\displaystyle t(n)}$, je rozdělení náhodné veličiny ${\displaystyle X={\frac {U}{\sqrt {\frac {V}{n}}}}}$, kde ${\displaystyle U}$ a ${\displaystyle V}$ jsou vzájemně nezávislé náhodné veličiny, přičemž ${\displaystyle U}$ má rozdělení ${\displaystyle \operatorname {N} (0,1)}$ a ${\displaystyle V}$ má rozdělení ${\displaystyle \chi ^{2}(n)}$.

Rozdělení ${\displaystyle t(n)}$ má pro ${\displaystyle -\infty <x<\infty }$ a ${\displaystyle n=1,2,3,...}$ hustotu pravděpodobnosti

${\displaystyle f(x)={\frac {\Gamma \left({\frac {n+1}{2}}\right)}{\Gamma \left({\frac {n}{2}}\right){\sqrt {\pi n}}}}{\left(1+{\frac {x^{2}}{n}}\right)}^{-{\frac {n+1}{2}}}}$

kde ${\displaystyle \Gamma }$ je gama funkce (zobecnění faktoriálu pro reálná čísla).

Střední hodnota rozdělení ${\displaystyle t(n)}$ je

${\displaystyle \operatorname {E} (X)=0}$

pro ${\displaystyle n>1}$.

Rozdělení ${\displaystyle t(n)}$ má rozptyl

${\displaystyle \sigma ^{2}(X)={\frac {n}{n-2}}}$

pro ${\displaystyle n>2}$.

Tabulka některých kvantilů pro některé počty stupňů volnosti:

Poznámka: protože t-rozdělení je symetrické, pro kvantily platí, že ${\displaystyle q_{p}=-q_{(1-p)}}$.

Poznámka: uvedené kvantily odpovídají kritickým hodnotám pro některé hladiny významnosti (používané například v t-testu), a to

• 95% kvantil – 10% hladina významnosti
• 97,5% kvantil – 5% hladina významnosti
• 99% kvantil – 2% hladina významnosti
• 99,5% kvantil – 1% hladina významnosti

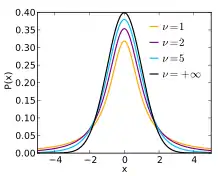
Pro hodnoty ${\displaystyle n>30}$ je rozdělení ${\displaystyle t}$ velmi blízké normovanému normálnímu rozdělení.

• T-test
• Normální rozdělení
• Rozdělení pravděpodobnosti

• Obrázky, zvuky či videa k tématu Studentovo rozdělení na Wikimedia Commons