Rolleova věta
Rolleova věta (též Rollova věta) je matematická věta diferenciálního počtu. Je pojmenována po francouzském matematikovi Michelu Rolleovi, který větu formuloval v roce 1691.

Věta
Nechť f je spojitá funkce na uzavřeném intervalu a nechť pro každý bod x otevřeného intervalu existuje derivace a nechť . Pak existuje bod c v otevřeném intervalu , pro nějž platí
- .
Důkaz
Důkaz rozdělíme do dvou částí:
- Nechť funkce f je konstantní. Potom derivace a věta je dokázána.
- Nechť funkce f není konstantní. Jelikož a funkce není konstantní, musí existovat takové, že nebo . Předpokládejme, že .
Využijeme věty tvrdící, že každá funkce spojitá na uzavřeném intervalu nabývá na tomto intervalu svého maxima i minima a zabývejme se maximem. Jelikož existuje takové, že , tak maximum nemůže ležet ani v a, ani v b. Leží tedy uvnitř intervalu, v bodě c. Z věty o nutné podmínce lokálního extrému vyplývá, že tedy v bodě c, kde se nalézá lokální extrém funkce, .
Analogické tvrzení platí i pro minimum.
Historie
Rolleovu větu znal už ve dvanáctém století indický matematik Bháskara II. První formální důkaz podal francouzský matematik Michel Rolle v roce 1691. Název Rolleova věta byl poprvé použit v devatenáctém století.
Příklady
První příklad
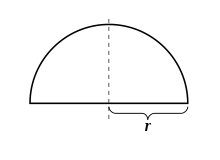
Buď poloměr a mějme funkci
.
Jejím grafem je horní půlkruh se středem v počátku. Tato funkce je spojitá na uzavřeném intervalu a má derivaci na otevřeném intervalu , ale ne v krajních bodech. Předpoklady Rolleovy věty jsou splněny, protože . A skutečně, bod s nulovou derivací existuje.

Druhý příklad
Pokud funkce nemá ve všech vnitřních bodech intervalu derivaci, nemusí závěr Rolleovy věty platit. Mějme funkci absolutní hodnoty:
.
Ačkoli , neexistuje žádný bod takový, že . Důvodem je právě to, že v bodě neexistuje derivace funkce .