Přirozená transformace

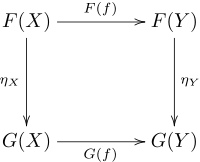
Mějme dvě kategorie ${\displaystyle {\mathcal {C}},{\mathcal {D}}}$ a dva funktory mezi nimi: ${\displaystyle F,G:{\mathcal {C}}\rightarrow {\mathcal {D}}}$. Přirozená transformace ${\displaystyle \eta }$ z ${\displaystyle F}$ do ${\displaystyle G}$ pak je soubor morfismů v kategorii ${\displaystyle {\mathcal {D}}}$ obsahující pro každé ${\displaystyle X\in {\mathcal {C}}}$ jednu složku ${\displaystyle \eta _{X}:F(X)\rightarrow G(X)}$, přičemž pro každý morfismus ${\displaystyle f:X\rightarrow Y}$ (v kategorii ${\displaystyle {\mathcal {C}}}$) platí

${\displaystyle G(f)\circ \eta _{X}=\eta _{Y}\circ F(f)}$.

Tato podmínka vyjadřuje, že existuje následující komutativní diagram (zobrazující morfismy v kategorii ${\displaystyle {\mathcal {D}}}$):

Jinými slovy, definice přirozené transformace říká, že pro každý morfismus ${\displaystyle f:X\rightarrow Y}$ v kategorii ${\displaystyle {\mathcal {C}}}$ existuje v kategorii ${\displaystyle {\mathcal {D}}}$ právě jeden morfismus ${\displaystyle F(X)\rightarrow G(Y)}$. V případě ${\displaystyle f=1_{X}}$ je tímto morfismem ${\displaystyle \eta _{X}}$, obecně pak výsledný morfismus tvoří diagonálu ve výše zobrazeném komutativním diagramu, která je jednoznačná právě díky komutativnosti tohoto diagramu (a přirozenou transformaci pak lze chápat jako mapování morfismů na komutativní čtverce).

V případě, že složky ${\displaystyle \eta _{X}}$ jsou pro každé ${\displaystyle X}$ izomorfismem, označuje se ${\displaystyle \eta }$ jako přirozený izomorfismus (též přirozená ekvivalence nebo ekvivalence funktorů).

Příkladem izomorfismu používaným ve funkcionálním programování je

${\displaystyle {\textrm {Hom}}(X\otimes Y,Z)\cong {\textrm {Hom}}(X,Z^{Y})}$.

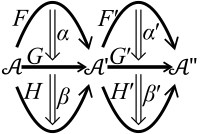
Přirozené transformace lze též skládat; existují přitom dva způsoby, jakým na sebe mohou skládané transformace navazovat, podle běžného způsobu znázornění na diagramu se tyto dva způsoby skládání označují jako vertikální a horizontální:

Jsou-li ${\displaystyle F,G,H:{\mathcal {A}}\rightarrow {\mathcal {A'}}}$ tři funktory mezi dvěma stejnými kategoriemi a ${\displaystyle \alpha :F\rightarrow G,\beta :G\rightarrow H}$ přirozené transformace mezi těmito funktory, pak můžeme tyto dvě transformace složit (vertikálně), přičemž platí

${\displaystyle (\beta \circ \alpha )_{X}=\beta _{X}\circ \alpha _{X}}$.

Vertikální skládání je tedy asociativní a má identitu (identitní přirozenou transformaci transformující funktor sám na sebe). Díky tomu se lze pro každou dvojici kategorií dívat na soubor všech funktorů spolu s přirozenými transformace mezi nimi jako na kategorii; viz kategorie funktorů.

Vedle toho můžeme definovat také horizontální skládání: máme-li dvě dvojice funktorů ${\displaystyle F,G:{\mathcal {A}}\rightarrow {\mathcal {A'}}}$ a ${\displaystyle F',G':{\mathcal {A'}}\rightarrow {\mathcal {A''}}}$ a dvě odpovídající přirozené transformace ${\displaystyle \alpha :F\rightarrow G}$ a ${\displaystyle \alpha ':F'\rightarrow G'}$, můžeme jejich horizontálním složením získat přirozenou transformaci ${\displaystyle (\alpha '*\alpha ):F'\circ F\rightarrow G'\circ G}$ mezi složenými funktory, jež je vzhledem k vlastnostem přirozených transformací dobře definovaná.

Horizontální a vertikální skládání lze kombinovat, neboť platí

${\displaystyle (\beta '\circ \alpha ')*(\beta \circ \alpha )=(\beta '*\beta )\circ (\alpha '*\alpha ):F'\circ F\rightarrow H'\circ H}$

Ve funkcionálním programování odpovídají funktorům (přesněji endofunktorům v kategorii typů daného programovacího jazyka a funkcí mezi nimi) generické typy, které poskytují operaci fmap mapující funkce na funkce. Přirozenou transformací pak je generická funkce mapující dva generické typy mezi sebou. Pokud například existují generické typy List<T> a Set<T>, odpovídá přirozené transformaci generická funkce List<T> → Set<T>. Podmínka komutativnosti přirozené transformace pak znamená, že dvě možnosti, jak provést konverzi např. z List<int> na Set<string> (buď nejprve zkonvertovat List<int> na List<string> pomocí fmap a následně zkonvertovat List<string> na Set<string> pomocí generické funkce pro transformaci, anebo naopak nejprve ztransformovat List<int> na Set<int> a poté aplikovat fmap pro konverzi Set<int> na Set<string>) musí dát stejný výsledek.

Přirozené transformace jsou také nedílnou součástí definice monád a monadických operátorů.

• LEINSTER, Tom. Basic Category Theory. Cambridge: Cambridge University Press, 2014. (Cambridge Studies in Advanced Mathematics; sv. 143). Bibcode 2016arXiv161209375L. arXiv:1612.09375 [math.CT]. Kapitola 1.3 Natural transformations, s. 27–38.