Oortovy konstanty

Oortovy konstanty se označují písmeny $A$ a $B$ . Vycházejí z Lindbladova-Oortova modelu, který předpokládá, že pohyb hvězd ve slunečním okolí lze vysvětlit jako rotaci okolo vzdáleného středu (galaktického centra). Jedná se tedy o pohyb uspořádaným způsobem kolmo na průvodič. Pro sluneční okolí jsou hodnoty

$A\approx 13\,\mathrm {km\,s^{-1}\,kpc^{-1}}$

$B\approx -13\,\mathrm {km\,s^{-1}\,kpc^{-1}}$

Odvození

V odvození se předpokládá, že okolní hvězdy jsou výrazně blíže ke Slunci než ke galaktickému středu. Lze se proto omezit pouze na lineární závislosti. Tento předpoklad je pro hvězdy do vzdálenosti 1 kpc dobře splněn. Dále se předpokládá, že je galaktický disk tenký a že je galaktická šířka pro okolní hvězdy blízká nule, tj. $b\approx 0$ .

Indexem $_{0}$ se označují proměnné vztažené ke Slunci. Definujme tedy vzdálenost Slunce od galaktického centra $R_{0}$ , okamžitou rychlost obíhání Slunce $\theta _{0}$ a úhlovou rychlost Slunce (z definice pro úhlovou rychlost tuhého tělesa)

$\omega _{0}={\frac {\theta _{0}}{R_{0}}}$ .

Schéma slunečního okolí

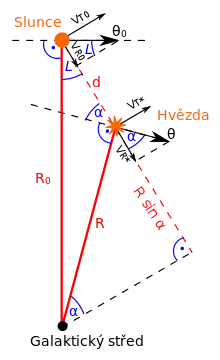
Uvažujme hvězdu ve vzdálenosti $d$ od Slunce a $R$ od galaktického středu s galaktickou délkou $l$ , která obíhá rychlostí $\theta$ a úhlovou rychlostí $\omega$ . Označme úhel, který svírá vektor rychlosti hvězdy se zorným paprskem $\alpha$ (viz obrázek).

První Oortova konstanta

Je zřejmé, že radiální rychlost hvězdy (tj. rychlost ve směru zorného paprsku) bude

$v_{R\star }=\theta \cos {\alpha }$ .

Víme-li navíc, že pohyb Slunce ve směru zorného paprsku je

$v_{R0}=\theta _{0}\sin {l}$ ,

můžeme zapsat relativní radiální rychlost hvězdy vůči Slunci jako

$v_{R}=\theta \cos {\alpha }-\theta _{0}\sin {l}$ .

Ze sinové věty pro trojúhelník s vrcholy Slunce, hvězdy a galaktický střed plyne

${\frac {\sin {(90^{\circ }+\alpha )}}{R_{0}}}={\frac {\sin {l}}{R}}$

${\frac {\cos {\alpha }}{R_{0}}}={\frac {\sin {l}}{R}}$

a tedy

$v_{R}=\left({\frac {\theta }{R}}-{\frac {\theta _{0}}{R_{0}}}\right)R_{0}\sin {l}=(\omega -\omega _{0})R_{0}\sin {l}$ .

Protože je $\omega (R)$ , použijeme na závorku v předchozím vztahu Taylorův rozvoj do lineárního členu.

$(\omega -\omega _{0})=\left({\frac {\mathrm {d} \omega }{\mathrm {d} R}}\right)_{0}(R-R_{0})$

Spočítáme derivaci

$\left({\frac {\mathrm {d} \omega }{\mathrm {d} R}}\right)_{0}={\frac {\mathrm {d} }{\mathrm {d} R}}\left({\frac {\theta }{R}}\right)_{0}={\frac {1}{R_{0}}}\left({\frac {\mathrm {d} \theta }{\mathrm {d} R}}\right)_{0}-\left({\frac {\theta }{R^{2}}}\right)_{0}$

a za již zmíněného předpokladu, že jsme v blízkosti Slunce, je

$R-R_{0}\approx -d\cos {l}$ .

Po dosazení dostaneme

$v_{R}=-\left[\left({\frac {\mathrm {d} \theta }{\mathrm {d} R}}\right)_{0}-\left({\frac {\theta }{R}}\right)_{0}\right]d\sin {l}\cos {l}={\frac {1}{2}}\left[{\frac {\theta }{R}}-{\frac {\mathrm {d} \theta }{\mathrm {d} R}}\right]_{0}d\sin {(2l)}$ .

První Oortovu konstantu definujeme předpisem

$A={\frac {1}{2}}\left[{\frac {\theta }{R}}-{\frac {\mathrm {d} \theta }{\mathrm {d} R}}\right]_{0}$ ,

pak lze relativní radiální rychlost zapsat také jako

$v_{R}=Ad\sin {(2l)}$ .

Druhá Oortova konstanta

Druhá Oortova konstanta souvisí s pohybem kolmo na směr zorného paprsku, neboli s tečnou složkou rychlosti. Pro hvězdu je tečná rychlost

$v_{T\star }=\theta \sin {\alpha }$

a pro Slunce je

$v_{T0}=\theta _{0}\cos {l}$ ,

je tedy zřejmé, že tečná rychlost hvězdy vzhledem ke Slunci je

$v_{T}=\theta \sin {\alpha }-\theta _{0}\cos {l}$ .

Z geometrie (viz obrázek) plyne

$R\sin {\alpha }+d=R_{0}\cos {l}$ .

Po dosazení dostaneme

$v_{T}=(\omega -\omega _{0})R_{0}\cos {l}-\omega d$

a díky tomu, že jsme v blízkosti Slunce, můžeme také psát

$\omega d=\omega _{0}d+(\omega -\omega _{0})d\approx \omega _{0}d$ .

Stejným postupem jako při odvozování Oortovy konstanty $A$ vyjde

$v_{T}=-\left[{\frac {\mathrm {d} \theta }{\mathrm {d} R}}-{\frac {\theta }{R}}\right]_{0}d\cos ^{2}{l}-\omega _{0}d={\frac {1}{2}}\left[{\frac {\theta }{R}}-{\frac {\mathrm {d} \theta }{\mathrm {d} R}}\right]_{0}d\cos {(2l)}-{\frac {1}{2}}\left[{\frac {\theta }{R}}+{\frac {\mathrm {d} \theta }{\mathrm {d} R}}\right]_{0}d$ .

Po zavedení druhé Oortovy konstanty předpisem

$B=-{\frac {1}{2}}\left[{\frac {\theta }{R}}+{\frac {\mathrm {d} \theta }{\mathrm {d} R}}\right]_{0}$

můžeme tečnou relativní rychlost zapsat jako

$v_{T}=Ad\cos {(2l)}+Bd$ .

Použití

Z Oortových konstant lze spočítat např. gradient rychlosti nebo úhlovou rychlost. Pro gradient rychlosti obě konstanty sečteme

$A+B=-\left({\frac {\mathrm {d} \theta }{\mathrm {d} R}}\right)_{0}\approx 0$ .

Nulový gradient je zde díky tomu, že v okolí Slunce jsou Oortovy konstanty $A\approx -B$ , z toho vyplývá, že je rotační křivka ve slunečním okolí plochá.

Odečtením konstant dostaneme úhlovou rychlost

$A-B=\left({\frac {\theta }{R}}\right)_{0}=\omega _{0}\approx 26\,\mathrm {km\,s^{-1}\,kpc^{-1}}$ ,

hodnota je opět pro Slunce. Z ní lze odhadnout periodu obíhání Slunce okolo středu Galaxie $T_{0}=250\,\mathrm {Myr}$ .

Externí odkazy

Obrázky, zvuky či videa k tématu Oortovy konstanty na Wikimedia Commons

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.