Metoda tečen
Metoda tečen je iterační numerická metoda užívaná v numerické matematice k nalezení kořenů funkce nebo k řešení soustavy nelineárních algebraických rovnic. Nazývá se také Newtonova metoda (nebo Newton-Raphsonova metoda) a metodou tečen je označována, protože přesnější řešení rovnice f(x) = 0 je hledáno ve směru tečny funkce f(x).

Popis algoritmu
Newtonova metoda tečen slouží k nalezení řešení rovnice f(x) = 0 za předpokladu, že známe derivaci funkce f'(x), tedy směrnici tečny. Pro jednoduchost dále předpokládejme, že x i f(x) jsou skaláry.
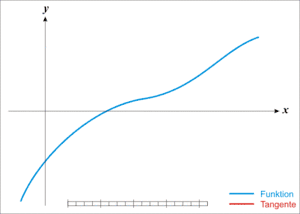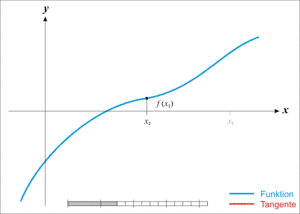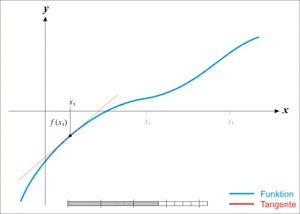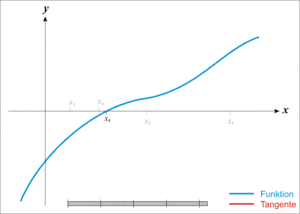
Dalším nezbytným předpokladem je znalost počáteční hodnoty x0, v jejíž blízkosti hledáme řešení. Pokud se funkce f(x) chová rozumně (je spojitá, hladká a monotónní v intervalu, ve kterém hledáme řešení), lze očekávat řešení v místě, kde tečna sestrojená z bodu f(x0) protíná osu x. (Směrnice této tečny je f'(x0).) Tento průsečík označíme x1 a vypočteme jej podle následujícího vztahu.
Za splnění výše uvedených předpokladů by měla hodnota f(x1) být blíže nule než původní f(x0). Stejný postup můžeme opakovat a najít tak ještě přesnější hodnotu xk.
Iteraci provádíme tak dlouho, dokud hodnota f(xk) neleží dostatečně blízko nuly.
Odvození vztahu pro řadu
Víme, že rovnice tečny tk funkce f(x) v libovolném bodě xk je dána vzorcem, jelikož derivace je směrnicí tečny (koeficient lineárního členu):
Zároveň také víme, že tečna tk prochází bodem . Po dosazení:
Hledáme bod , což je průnik tečny tk v bodě xk s osou x, a zároveň dosadíme vyjádřené b:
Odtud již plyne:
Příklad: Výpočet druhé odmocniny
Úkolem je vypočítat druhou odmocninu kladného reálného čísla a.
Problém lze definovat také jako nalezení kořenu funkce , neboli řešení rovnice .
Vypočteme derivaci .
Dosadíme do obecného vzorce a upravíme.
Získáváme tak rekurentní rovnici, u které jako počáteční podmínku můžeme zvolit .
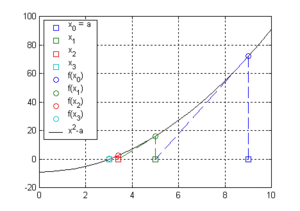
Výpočet (druhé odmocniny z devíti) bude podle výše uvedeného algoritmu probíhat následovně.
a = 9 x0 = 9 x1 = 5 x2 = 3.4 x3 = 3.02352941176471 x4 = 3.00009155413138 x5 = 3.00000000139698 x6 = 3.00000000000000 x7 = 3.00000000000000
Je vidět, že po několika málo krocích se hodnota nemění a ustálí se (konverguje) na hodnotě 3, což odpovídá správnému výsledku.
Poznámky
Aproximace derivace
Pokud známe pouze funkci f(x) a neznáme její derivaci f'(x), můžeme se pokusit derivaci nahradit numerickou derivací. Případně je možné řešit úlohu metodou sečen, která znalost derivace nevyžaduje.
Vektory
Je-li funkce f(x) skalární funkcí vektorového argumentu („z vektoru vypočte skalár“), je nutné hledat xk+1 proti směru gradientu. Předpis pro iteraci lze potom napsat následovně.
Pokud je funkce f(x) vektorovou funkcí vektorového argumentu („z vektoru vypočte vektor“), lze předpis pro iteraci napsat následovně.
Matice J je takzvaná Jacobiho matice obsahující parciální derivace.
Související články
- Fraktál Newton – fraktál generovaný Newtonovou metodou
- Linearizace – jedním ze způsobů linearizace je nahrazení části křivky její tečnou
Externí odkazy
 Obrázky, zvuky či videa k tématu Metoda tečen na Wikimedia Commons
Obrázky, zvuky či videa k tématu Metoda tečen na Wikimedia Commons - Newtonova metoda: http://math.fce.vutbr.cz/vyuka/matematika/numericke_metody/node10.html
- Řešení rovnic, Newtonova metoda: https://web.archive.org/web/20071031001614/http://vydra.troja.mff.cuni.cz/bobo/fyzika/num3_metodanewtonova.cz