Metoda Lagrangeových multiplikátorů

Metoda Lagrangeových multiplikátorů neboli Lagrangeova metoda neurčitých koeficientů je metoda, jak nalézt extrémy diferencovatelné funkce za předpokladu platnosti diferencovatelných omezujících podmínek. Uveřejnil ji Joseph-Louis Lagrange počátkem 19. století.

Lagrange

Jestliže hledáme extrémy funkce $f\left(x_{1},\ldots ,x_{n}\right)$ za předpokladu platnosti m vazeb (omezujících podmínek) ve tvaru

g_{k}\left(x_{1},\ldots ,x_{n}\right)=0,

kde n a k jsou přirozená čísla a k nabývá hodnot mezi 1 a m, tak metoda Lagrangeových multiplikátorů začíná vytvořením Lagrangeovy funkce ${\mathcal {L}}$ , závislé na n + m proměnných:

{\mathcal {L}}\left(x_{1},\ldots ,x_{n},\lambda _{1},\ldots ,\lambda _{m}\right)=f\left(x_{1},\ldots ,x_{n}\right)+\sum \limits _{k=1}^{m}{\lambda _{k}g_{k}\left(x_{1},\ldots ,x_{n}\right)}.

Kromě původních proměnných $x_{1},\ldots ,x_{n}$ tedy zavádíme další neznámé $\lambda _{1},\ldots ,\lambda _{m}$ , zvané Lagrangeovy multiplikátory. Nyní platí, že pokud se hledaný vázaný extrém nalézá v bodě, kde jsou všechny zkoumané funkce diferencovatelné, pak tento bod splňuje kromě m vazebných rovnic uvedených výše také n rovnic tvaru

{\frac {\partial {\mathcal {L}}}{\partial x_{i}}}=0,

což je totéž jako

{\frac {\partial f}{\partial x_{i}}}=\sum _{k=1}^{m}\lambda _{k}{\frac {\partial g_{k}}{\partial x_{i}}}.

Tím získáme soustavu n + m rovnic pro n + m proměnných, jejímž řešením najdeme potenciální extrémy. Pak je potřeba vyšetřit, zda se jedná o maxima, minima nebo sedlové body. V případě, že zúčastněné funkce vykazují nediferencovatelné body, je potřeba zvlášť vyšetřit i tyto, neboť i zde se mohou hledané extrémy nacházet.

Poněvadž m vazebných podmínek lze získat tím, že Lagrangeovu funkci parciálně zderivujeme podle multiplikátorů a derivace položíme rovny nule, lze souhrnně říci, že nutnou podmínkou existence vázaného extrému za podmínek diferencovatelnosti v daném bodě je, aby gradient Lagrangeovy funkce v tomto bodě vymizel, což lze vektorově zapsat jako:

\nabla _{\mathbf {x} ,{\boldsymbol {\lambda }}}{\mathcal {L}}(\mathbf {x} ,{\boldsymbol {\lambda }})=0,

což znamená, že Lagrangeovu funkci je potřeba postupně zderivovat podle všech jejích n + m proměnných, derivace položit rovny nule a soustavu vyřešit. Řešení udávají souřadnice bodů, v nichž může (ale nemusí) existovat hledaný vázaný extrém.

Příklad

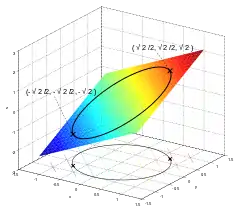
Extrémní hodnoty lineární fukce na kružnici

Najděme maximum lineární funkce $f(x,y)=x+y$ vázané na jednotkovou kružnici $x^{2}+y^{2}=1$ .

Vazba je

g(x,y)=x^{2}+y^{2}-1,

takže Lagrangeova funkce je

{\begin{aligned}{\mathcal {L}}(x,y,\lambda )&=f(x,y)+\lambda \cdot g(x,y)\\&=x+y+\lambda (x^{2}+y^{2}-1).\end{aligned}}

Derivací Lagrangeovy funkce podle jednotlivých proměnných získáme gradient:

{\begin{aligned}\nabla _{x,y,\lambda }{\mathcal {L}}(x,y,\lambda )&=\left({\frac {\partial {\mathcal {L}}}{\partial x}},{\frac {\partial {\mathcal {L}}}{\partial y}},{\frac {\partial {\mathcal {L}}}{\partial \lambda }}\right)\\&=\left(1+2\lambda x,1+2\lambda y,x^{2}+y^{2}-1\right)\end{aligned}}

a jeho položením rovna nule dostaneme soustavu tří rovnic pro tři neznámé proměnné:

\nabla _{x,y,\lambda }{\mathcal {L}}(x,y,\lambda )=0\quad \Leftrightarrow \quad {\begin{cases}1+2\lambda x=0\\1+2\lambda y=0\\x^{2}+y^{2}-1=0.\end{cases}}

Poslední rovnice je vazba, z prvních dvou rovnic dostaneme

x=y=-{\frac {1}{2\lambda }},\qquad \lambda \neq 0.

Dosazením do poslední rovnice máme

{\frac {1}{4\lambda ^{2}}}+{\frac {1}{4\lambda ^{2}}}-1=0,

takže

\lambda =\pm {\frac {1}{\sqrt {2}}},

což po dopočítání x a y vede k závěru, že řešení (stacionární body ${\mathcal {L}}$ ) jsou

\left({\tfrac {\sqrt {2}}{2}},{\tfrac {\sqrt {2}}{2}},-{\tfrac {1}{\sqrt {2}}}\right),\qquad \left(-{\tfrac {\sqrt {2}}{2}},-{\tfrac {\sqrt {2}}{2}},{\tfrac {1}{\sqrt {2}}}\right).

Vypočítáme hodnoty $f$ v těchto bodech (zajímají nás jen první dvě souřadnice stacionárních bodů, třetí souřadnice odpovídá multiplikátoru, který v tuto chvíli už nepotřebujeme):

f\left({\tfrac {\sqrt {2}}{2}},{\tfrac {\sqrt {2}}{2}}\right)={\sqrt {2}},\qquad f\left(-{\tfrac {\sqrt {2}}{2}},-{\tfrac {\sqrt {2}}{2}}\right)=-{\sqrt {2}}.

Vázané maximum tedy je ${\sqrt {2}}$ a vázané minimum $-{\sqrt {2}}$ .

Geometrický význam

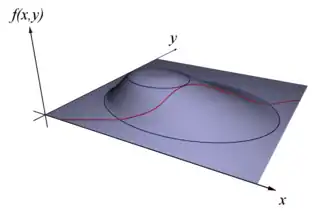
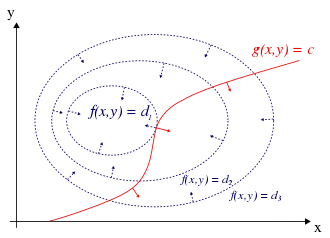
Funkce dvou proměnných f(x, y) je znázorněna fialovou plochou. Úlohou je najít maximální hodnotu této funkce ležící na červené vazebné křivce g(x, y) = 0 (vázaný extrém). Modré ovály jsou „vrstevnice“ funkce f, tedy geometrická místa s konstantní hodnotou funkce; menší modrý ovál je vrstevnice, na které leží vázaný extrém.

Půdorys situace znázorněné na předchozím grafu. Je vidět, že vrstevnice, na které leží vázaný extrém, se dotýká křivky g v bodě, v němž obě křivky mají stejný směr – stejnou tečnu

Ve dvourozměrném případě na obrázcích je naznačena funkce f a její vrstevnice f(x, y) = 0, jakož i křivka g(x, y) = 0 odpovídající vazbě. Hledáme nejvyšší hodnotu f, která se nachází na bodech této červeně vyznačené křivky (tj. vázaný extrém).

Vázaný extrém se může vyskytnout pouze na vrstevnici, kterou křivka vazby neprotíná. Jinak totiž se na jedné straně od takové vrstevnice nacházejí hodnoty vyšší a na druhé straně nižší než f(x, y), a proto zde nemůže nastat extrém; postupem po křivce vazby se totiž hned v sousedství daného bodu dostaneme na hodnoty vyšší nebo nižší než v tomto bodě.

Pokud se vrstevnice a křivka vazby neprotínají, musejí se dotýkat (být si lokálně tečnami). Stačí tedy analyticky vyjádřit, že se dvě křivky dotýkají, a máme nutnou podmínku vázaného extrému. K tomu účelu si uvědomme, že „lokální směr“ přímky nebo plochy určuje gradient – vektor, mířící ve směru největšího zakřivení, a tedy kolmý na tečnu. Na nižším obrázku jsou gradienty naznačeny jako malé šipky vycházející z křivek.

Protože tečny jsou stejné, musejí být až na měřítko shodné i gradienty – musejí mířit stejným (anebo přesně opačným) směrem. Existuje tedy nenulová konstanta $\lambda$ tak, že v bodě dotyku (x, y) platí

\nabla f=\lambda \cdot \nabla g

neboli

\nabla f-\lambda \cdot \nabla g=0,

kde $\nabla f$ je gradient $f$ v tomto bodě a $\nabla g$ je gradient $g$ tamtéž. Souřadnice gradientů dostaneme jako parciální derivace příslušných funkcí podle jednotlivých souřadnic, což umožní uvedenou vektorovou rovnici rozepsat po souřadnicích:

\left\{{\begin{array}{llcc}{\dfrac {\partial f}{\partial x}}{\Big |}_{(x,\;y)}&-\lambda \cdot {\dfrac {\partial g}{\partial x}}{\Big |}_{(x,\;y)}&=&0\\{\dfrac {\partial f}{\partial y}}{\Big |}_{(x,\;y)}&-\lambda \cdot {\dfrac {\partial g}{\partial y}}{\Big |}_{(x,\;y)}&=&0.\\\end{array}}\right.

Pokud k těmto dvěma rovnicím připojíme ještě třetí, vazební rovnici g(x, y) = 0, dostaneme přesně totéž, co bychom získali parciálním derivováním příslušné Lagrangeovy funkce

{\begin{aligned}{\mathcal {L}}(x,y,\lambda )&=f(x,y)+\lambda \cdot g(x,y)\\\end{aligned}}

podle všech tří jejích argumentů a položením jednotlivých derivací rovných nule.

Tato úvaha není důkazem v přísném smyslu, protože se opírá o geometrickou intuici a neřeší různé zvláštní případy (zejména co se stane, když některý z gradientů vymizí – je roven nulovému vektoru). Lze ji však snadno zobecnit na více proměnných a vazeb, a odůvodnit tak obecnou Lagrangeovu metodu.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.