Kumulativní četnost
Kumulativní četnost je postupně načítaná četnost jednotlivých vzestupně uspořádaných hodnot statistického znaku ve statistickém souboru.[1]
Absolutní a relativní hodnota kumulativní četnosti
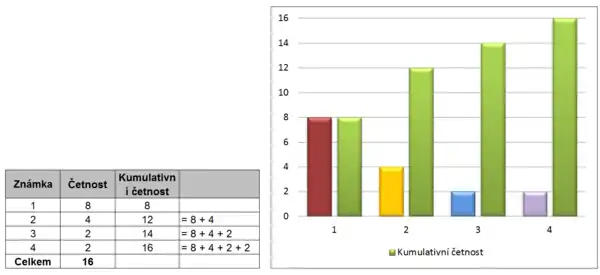
V případě, že náš sledovaný statistický znak nabývá mnoha různých hodnot, potom si je můžeme rozdělit do několika intervalů, kterým říkáme třídy[2]. Počet tříd udává Sturgesovo pravidlo.[3] V případě, že statistický znak je omezená množina jako v níže uvedeném příkladu, potom její hodnoty mohou být přímo třídami. Absolutní hodnota četnosti vyjadřuje kolikrát se daná hodnota znaku z našeho statistického souboru v každé třídě vyskytuje. [4] Absolutní hodnota kumulativní četnosti je potom součtem všech hodnot všech absolutních četností sledované třídy a všech nižších tříd. Relativní hodnota kumulativní četnosti je potom přepočtena na počet prvků souboru. Udává se obvykle v procentech.
Příklad
Mějme školní třídu 16 žáků a jejich známky z matematiky. V terminologii statistiky máme statistický soubor o rozsahu 16 statistických jednotek. Statistický znak který u našich jednotek sledujeme je jejich známka z matematiky. Spočteme kolik žáků má kterou známku, vyjádřili jsme četnost výskytu známek.
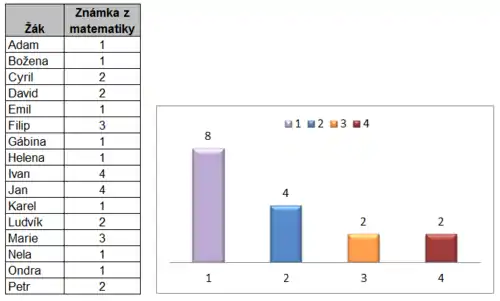
Absolutní kumulativní četnost – výpočet a vyjádření v grafu.
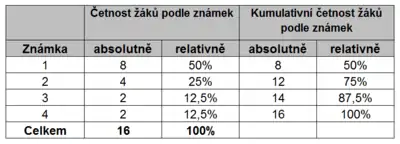
Praktické použití
Kumulativní četnost se spolu s dalšími statistickými metodami používá v mnoha oborech lidské činnosti. Příkladem může být biomedicínský výzkum[5], nebo při řízení kvality v Paretově diagramu.
Odkazy
Reference
- Kumulativní četnost - definice
- fzp.ujep.cz/~synek/statistika/prednasky/LESS1POP2.DOC Univerzita Jana Evangelisty Purkyně - Statistika, přednášky
- en:Freedman–Diaconis rule
- Matematika polopatě : Základy statistiky. www.matweb.cz [online]. [cit. 2012-11-21]. Dostupné v archivu pořízeném z originálu dne 2013-01-05.
- Statistické metody v biomedicínském výzkumu. ulb.upol.cz [online]. [cit. 2013-06-20]. Dostupné v archivu pořízeném dne 2013-06-20.
Literatura
- HENDL, Jan. Přehled statistických metod zpracování dat. Praha: Portál, 2004. ISBN 80-7178-820-1.
- SHULTZ, Kenneth S.; WHITNEY, David J. Measurement Theory in Action: Case Studies and Exercises. Thousand Oaks: Sage Publications, 2004. Dostupné online. ISBN 978-0761927303. (anglicky)
- OTIPKA P., ŠMAJSTRLA V., Pravděpodobnost a statistika, VŠB – TU Ostrava