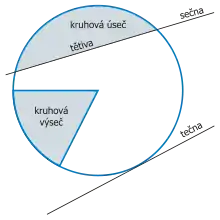
Kruhová úseč
Kruhová úseč je část kruhu vymezená tětivou a kruhovým obloukem vzniklá rozdělením kruhu sečnou.
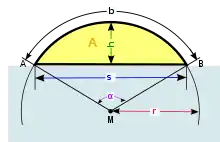
M – střed kružnice,
r – poloměr kružnice,
AB – tětiva,
s – délka tětivy,
h – výška úseče,
α – středový úhel,
b – délka oblouku,
A – obsah úseče
Každá úseč je příslušná středovému úhlu α, který může být konvexní (0° < α < 180°), konkávní (180° < α < 360°), nebo přímý (α = 180°; polokruh).
Obvod úseče, poloměr, tětiva a výška
Použité značení:
- r – poloměr kruhu
- α – středový úhel, ; ; ; ;
- s – délka tětivy, ;
- h – výška oblouku, ; ;
- ; ; ;
- ; ;
- b – délka oblouku: (arc = úhel v radiánech); ; (pro nastavení kalkulačky na stupně); (pro nastavení kalkulačky na stupně)
Obvod kruhové úseče:
- (arc = úhel v radiánech)
- (arc = úhel v radiánech)
- (pro nastavení kalkulačky na stupně)
V případě, že je úhel α konvexní (0 < α < π), je obsah úseče roven obsahu výseče () bez obsahu rovnoramenného trojúhelníka (; kladné číslo).
V případě, že je úhel konkávní (π < α < 2π), je obsah úseče roven obsahu výseče a obsahu rovnoramenného trojúhelníka. Pro konkávní středový úhel ovšem vyjde obsah trojúhelníka () záporný, takže pro celkový obsah úseče opět platí předchozí vzorec:
Známe-li výšku úseče a poloměr:
V praxi je úseč často určena šířkou (délka tětivy) a výškou . Pro obsah pak platí
Literatura
- Martina Palková a kolektiv: Průvodce matematikou 2, Didaktis, Brno 2007, ISBN 978-80-7358-083-4, str. 30