Heavisideova funkce

Heavisideova funkce (také jednotkový skok) je nespojitá funkce, jejíž hodnota je nulová pro zápornou hodnotu argumentu a rovna jedné pro kladnou hodnotu argumentu. Hodnota funkce pro nulový argument není podstatná a proto je různými autory definována odlišně (viz níže).

H₁(x)

H_1/2(x)

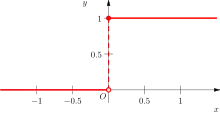
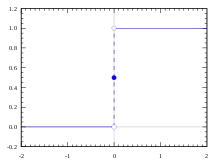
Často se používá v teorii řízení a při zpracování signálu, kde slouží k reprezentaci jednorázové změny signálu. Pojmenována byla po anglickém učenci Oliveru Heavisideovi.

Definice

Heavisidova funkce (s parametrem p) se definuje předpisem:

H_{p}(x)=\left\{{\begin{matrix}0&{\mbox{ pro }}x<0\\p&{\mbox{ pro }}x=0\\1&{\mbox{ pro }}x>0\end{matrix}}\right.

,

kde 0 ≤ p ≤ 1 je reálné číslo určující hodnotu funkce v bodě 0 (platí $p=H_{p}(0)$ ).

Index p je většinou volen pevně a v zápise se vynechává. Heavisidova funkce se potom značí pouze H(x).

Hodnota v nule

Parametr $p$ z definice funkce se nejčastěji volí jako 0, 1/2 nebo 1. Pro hodnotu 1/2 svědčí symetrie výsledné funkce a fakt, že hodnota zpětné transformace Fourierova obrazu funkce v bodech nespojitosti je aritmetický průměr limit zleva a zprava. Důvodem jiné volby může být praktičnost při jistých způsobech použití. V mnoha případech na hodnotě v nule vůbec nezáleží, např. integrujeme-li složený výraz s touto funkcí, neboť Lebesgueova míra množiny $\{0\}$ je nulová.

Nastavíme-li $p=H(0)=1/2$ , můžeme definovat funkci pomocí znaménkové funkce (signum):

H(x)={\frac {1+\operatorname {sgn}(x)}{2}}

Pro případ, kdy $p=1$ nebo $p=0$ můžeme též chápat Heavisideovu funkci takto: $H_{1}=\chi _{\langle 0,\infty )}$ respektive $H_{0}=\chi _{(0,\infty )}$ kde $\chi _{M}$ značí charakteristickou funkci množiny $M$ .

Vlastnosti

Mezi jednotkovým skokem a Diracovou funkcí existuje vztah, který lze zapsat jako

H(x)=\int _{-\infty }^{x}\delta (t)\mathrm {d} t

Derivací Heavisideovy funkce je tedy Diracova delta funkce, primitivní funkcí je tzv. náběhová funkce.

Odkazy

Související články

Externí odkazy

Obrázky, zvuky či videa k tématu Heavisideova funkce na Wikimedia Commons
(anglicky) MathWorld, Heaviside Step Function: http://mathworld.wolfram.com/…
(anglicky) PlanetMath, Heaviside step function: http://planetmath.org/… Archivováno 2. 2. 2009 na Wayback Machine
(anglicky) MathWorks, Heaviside: http://www.mathworks.com/…

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.