Eukleidova věta
Eukleidova věta je označení pro dvě geometrická tvrzení o vlastnostech trojúhelníku, pojmenované po svém objeviteli, řeckém matematikovi Eukleidovi.
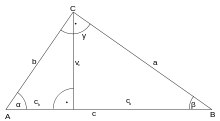
Eukleidova věta o výšce
Obsah čtverce sestrojeného nad výškou pravoúhlého trojúhelníku je roven obsahu obdélníku sestrojeného z obou úseků přepony.
Důkaz 1
Označíme-li P patu kolmice z bodu C na přeponu AB, tvrzení vyplývá z podobnosti trojúhelníků APC a CPB:
Větu lze rovněž dokázat pomocí Pythagorovy věty, z ní plyne:
Rovnice sečteme:
upravíme první 2 členy podle Pythagorovy věty:
rozepíšeme a roznásobíme dvojmoc přepony, odečteme dvojmoci jejích úseků:
a vydělíme dvěma:
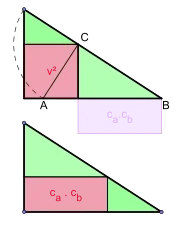
Důkaz s využitím Pythagorovy věty není zdaleka jediným. Tvrzení lze elementárně dokázat pomocí podobnosti trojúhelníků, v Eukleidových Základech je tato rovnosti obsahů čtverce a obdélníka dokázána v druhém díle (Kniha II, tvrzení 14). Nejjednodušší je důkaz přerovnáním shodných útvarů.
Důkaz 2
V pravoúhlém trojúhelníku ABC sestrojíme růžový čtverec nad výškou v a obdélník se stranami ca a cb. Doplníme obrázek do velkého pravoúhlého trojúhelníku. Velký trojúhelník je poskládán dvojím způsobem. Čtverec nad odvěsnou o obsahu je ve druhém rozkladu nahrazen obdélníkem o obsahu . Odtud růžové objekty musí mít stejný obsah.
Eukleidova věta o odvěsně
Obsah čtverce sestrojeného nad odvěsnou pravoúhlého trojúhelníku je roven obsahu obdélníku sestrojeného z přepony a úseku přepony k této odvěsně přilehlé.
Důkaz 1
Předpokládáme, že platí Euklidova věta o výšce (důkaz viz výše), z Pythagorovy věty plyne:
Pro druhou odvěsnu plyne z principu záměny (symetrie) odvěsen.

Podobně jako u předcházející věty je možné tvrzení dokázat pomocí podobnosti trojúhelníků, nebo přerovnáním shodných útvarů. V Eukleidových Základech je tato rovnosti obsahů čtverce a obdélníka naopak součásti důkazu Pythagovy věty (Kniha I, tvrzení 47).
Důkaz 2
Pro zelený pravoúhlý trojúhelník ABC sestrojíme růžový čtverec nad odvěsnou b = AC a obdélník se stranami c a cb. Doplníme obrázek šedými pomocnými trojúhelníky. Obsah velkého trojúhelníku je poskládán dvojím způsobem. Čtverec nad odvěsnou o obsahu je nahrazen obdélníkem o obsahu .
Délka výšky
Na základě znalosti Eukleidových vět a daných délek stran a a b lze vypočítat délku výšky:
Příklad
Mějme pravoúhlý trojúhelník se stranami (v libovolných, ale shodných jednotkách). Vypočítejte výšku .
Platí:
Po dosazení do druhého vzorce:
Dopočet :
Po dosazení do prvního vzorce:
Výška tohoto trojúhelníku je přibližně 3,9.