Asymptotická volnost

Asymptotická volnost byl popsána a publikována v roce 1973 Davidem Grossem a Frankem Wilczekem a také Davidem Politzerem. I když tito autoři byli první, kdo pochopil fyzikální význam silné interakce, již v roce 1965 objevili V. S. Vanyashin a M. V. Terentev asymptotickou volnost v kvantové elektrodynamice u nabitých vektorových polí[4] a v roce 1969 Josif Chriplovič v SU(2) kalibrační teorii teorie.[5] Gerardus 't Hooft v roce 1972 také poukázal na existenci efektu, ale svoji práci nezveřejnil.[6] Za objev získali Gross, Wilczek a Politzer Nobelovu cena za fyziku pro rok 2004.

Objev byl důležitý při obnově kvantové teorie pole. Před rokem 1973 měli mnozí teoretici podezření, že teorie pole je zásadně nekonzistentní, protože se interakce stávají nekonečně silnými na krátkých vzdálenostech. Tento jev se obvykle nazývá Landaův pól, a definuje nejmenší délkové měřítko, které může teorie popsat. Tento problém byl objeven v oblasti teorie interakce skalárních veličinách a spinorů, včetně kvantová elektrodynamiky a Lehmanovy pozitivity, což vedlo mnohé k podezření, že je to nevyhnutelné.[7] Asymptoticky volné teorie se stávají slabými na krátké vzdálenosti, není přítomen žádný Landaův pól, a tyto kvantové teorie pole jsou, jak se věří zcela konzistentní pro libovolnou délku stupnice.

Standardní model není asymptoticky volný, s Landauovým pólem je problém vzhledem k Higgsově bosonu. Kvantová trivialita může být použita k omezení nebo předpovědi parametrů, jako je hmotnost Higgsova bosonu. To vede k předvídatelné hmotnost Higgsova bosonu ve scénářích asympotické bezpečnosti. V dalších scénářích jsou interakce slabé tak, že jakékoli nesrovnalosti vznikají ve vzdálenostech kratších než Planckova délka.

Stínění náboje v QED

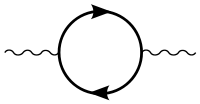
Změny ve fyzikální vazebné konstantě v rámci změny rozsahu lze chápat kvalitativně jako pocházející z akčního pole virtuálních částic nesoucích příslušný náboj. Chování Landauova pólu v kvantové elektrodynamice (QED, týkající se kvantové triviality) je důsledkem stínění virtuálních párů částice-antičístice, jako jsou elektron-pozitronové páry, ve vakuu. V okolí náboje se vakuum stává polarizované: virtuální částice protichůdného náboje jsou přitahovány k náboji a virtuální částice shodného náboje jsou odpuzovány. Čistý efekt je částečné vyrušení pole v nějaké konečné vzdálenosti. Stále blíže a blíže k centrální náboji lze vidět méně a méně účinku vakua a efektivní zvyšování náboje.

V kvantové chromodynamice se totéž děje s virtuálními páry kvarků a antikvarků, které mají tendenci projevovat barevný náboj. Nicméně v případě kvantové chromodynamiky její částice, zodpovědné za přenos síly, gluony samy nesou barevný náboj. Každý gluon nese barevný náboj a antibarevný magnetický moment. Čistý efekt polarizace virtuálních gluonů ve vakuu se neprojevuje na poli, ale rozšířuje a mění jeho barvu. To se někdy nazývá antistínění. Blíže ke kvarku se snižuje vliv antistínění na okolní virtuální gluony, takže tento efektu oslabuje efektivní náboj s klesající vzdáleností.

Virtuální kvarky a virtuální gluony přispívají opačnými účinky, takže efekt výhry závisí na počtu různých druhů nebo vůní kvarků. Pro standardní kvantovou chromodynamiku se třemi barvami existuje ne více než 16 vůní kvarků (nepočítaje antikvarky samostatně), antistínění převládá a teorie je asymptoticky volná. Ve skutečnosti je jen 6 známý vůní kvarků.

Asymptotickou volnost lze odvodit pomocí výpočtu beta-funkce popisující odchylky vazebná konstanty teorie v rámci renormalizační grupy. Pro dostatečně krátké vzdálenosti, nebo velké výměny hybnosti (které sondují krátkou vzdálenost chování, protože platí inverzní vztah mezi kvantovou hybností a De Broglieho vlnovou délkou), jde o asymptoticky volnou teorii podléhající perturbační teorii, kde se výpočty provádějí pomocí Feynmanových diagramů. Takové situace jsou proto teoreticky tvárné více než dlouhé vzdálenosti a silně propojené chování je také často přítomné v takových teoriích, což vytváří uvěznění kvarků.

Výpočet beta-funkce je záležitost vyhodnocení Feynmanových diagramů, které přispívají k interakci emitace kvarků nebo absorpce gluonů. V podstatě beta-funkce popisuje, se vazebné konstanty liší jako jednoškálový systém ${\displaystyle x\rightarrow bx}$. Výpočet lze provést pomocí změny škálování v pozici prostoru nebo dynamiku prostoru. V neabelovské kalibrační teorii jako kvantová chromodynamika závisí existence asymptotické volnosti na kalibrační grupě a počte vůní interakce částic. Pro nejnižší netriviální pořadí, beta-funkce v SU(N) kalibrační teorii s ${\displaystyle n_{f}}$ druhy kvarků je

${\displaystyle \beta _{1}(\alpha )={\alpha ^{2} \over \pi }\left(-{11N \over 6}+{n_{f} \over 3}\right)}$

kde ${\displaystyle \alpha }$ je ta teoretický ekvivalent konstanty jemné struktury, ${\displaystyle g^{2}/(4\pi )}$ v jednotkách oblíbených částicovými fyziky. Je-li tato funkce negativní, teorie je asymptoticky volná. Pro SU(3) má ${\displaystyle N=3,}$ a podmínku, že ${\displaystyle \beta _{1}<0}$ dává

${\displaystyle n_{f}<{33 \over 2}.}$

Tedy pro SU(3), barevný náboj kalibrační grupy teorie kvantové chromodynamiky je asymptoticky volná, pokud existuje 16 nebo méně vůní kvarků.

Kromě kvantové chromodynamiky, může být asymptotická volnost pozorována i v jiných systémech jako je nelineární ${\displaystyle \sigma }$-model ve 2 rozměrech, který má strukturu podobnou SU(N) invariantní Yangově-Millsově teorii ve 4 rozměrech.

A konečně, lze nalézt teorie, které jsou asymptoticky volné a redukovatelné na kompletní Standardní model elektromagnetické, slabé a silné interakce pro dostatečně nízké energie.[8]

V tomto článku byl použit překlad textu z článku Asymptotic freedom na anglické Wikipedii.