Polarizace vakua

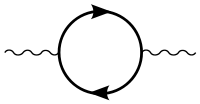
U elektromagnetické interakce je zdrojovým nábojem elektrický náboj. Pole kolem něj si lze představit jako oblak virtuálních fotonů. Polarizaci vakua si lze v kvantové elektrodynamice představit tak, že se foton promění na elektron-pozitronový pár (jak ukazuje schéma na obrázku vpravo) na dobu řádově danou relací neurčitosti pro čas a energii (τ, E, ℏ jsou střední doba života, energie a Planckova konstanta):

${\displaystyle \Delta \tau \ \Delta E\sim \hbar }$.

(Virtuálním párem může být i mion-antimion, tauon-antitauon či kvark-antikvark, zde jsou však energie řádově větší a proto i efektivní doby, po které se mohou na polarizaci podílet, a tedy i jejich vliv řádově menší.) Zdrojový náboj pole pak opačně nabitou částici páru přitahuje a souhlasně nabitou odpuzuje. Vytvoří se tak dipól aspoň částečně orientovaný tak, že podobně jako při polarizaci dielektrika vytváří opačně orientované elektrické pole, které zdrojové pole částečně stíní. Zdrojový náboj se tak jeví menší.[1]

Na makroskopických vzdálenostech je efektivní elektrický náboj částic s jednotkovým elementárním nábojem stíněný polarizací vakua roven známé konstantě značené e a rovné 1,602 176 6208(98)×10⁻¹⁹ C.[2] Odpovídající vazebná konstanta elektromagnetické interakce je známa jako konstanta jemné struktury, v soustavě SI definované vztahem:

${\displaystyle \alpha _{\mathrm {e} }={\frac {e^{2}}{4\pi \varepsilon _{0}\hbar c}}}$

a rovné 7,297 352 5664(17)×10⁻³ = 1/137,035 999 139(31).[2] Interakce na kratších vzdálenostech r, což odpovídá vyšším hybnostem q předávaným při interakci (q~1/r), je nejen silnější z důvodů nárůstu Coulombova potenciálu, ale má vzhledem k nižšímu stínění polarizací vakua vyšší i vazebnou konstantu interakce, tedy zdrojový náboj se jeví větší. Pro hybnosti značně větší než m_ec, kde m_e je klidová hmotnost elektronu, roste vazebná konstanta α_e(q) logaritmicky s q. Pro hybnost m_Zc (m_Z je klidová hmotnost intermediálního bosonu Z) odpovídající vzdálenosti řádově 10⁻¹⁹ m je například vazebná konstanta α_e rovna 1/127,916(15).[3]

U silné (barevné) interakce je zdrojem pole barevný náboj, mající 3 různé hodnoty a jim odpovídající antihodnoty (v tradiční názorné reprezentaci červená, modrá, zelená, antičervená, antimodrá, antizelená). Interakci zprostředkují gluony 8 barevných "druhů", nesoucí také barevný náboj (8 nezávislých lineárních kombinací z barevných stavů, které se někdy označují jako červeno-antimodrý, červeno-antizelený, červeno-antičervený apod., třebaže tato reprezentace matematických vztahů v barevné grupě SU(3)_c již může být poněkud zavádějící). Polarizace vakua je dvojího druhu:[4]

Virtuální gluony kolem zdrojového kvarku s daným barevným nábojem se mohou na čas řádově daný principem neurčitosti proměnit na virtuální pár kvark-antikvark opačného náboje a podobně jako u elektromagnetické interakce přispívat k dílčímu stínění zdrojového náboje.

Protože však gluon je sám nositelem barevného náboje, může být i zdrojem dalších virtuálních gluonů. V názorné interpretaci kvantové chromodynamiky je to přesněji vyjádřeno tím, že pro silnou interakci jsou přípustné i Feynmanovy diagramy s uzly, ve kterých se setkávají tři nebo čtyři výhradně gluonové linie, jak ukazují obrázky vpravo.) Tento fakt je příčinou tzv. antistínění, tedy růstu efektivní vazebné konstanty silné interakce s rostoucí vzdáleností. Kvantově chromodynamické výpočty ukazují, že stínění roste s počtem kvarkových vůní (dnes se má za to, že je jich právě 6), antistínění s počtem odlišných zprostředkujících bosonů (tedy právě 8 druhů gluonů). V konečném důsledku je antistínění asi o řád účinnější než stínění a vazebná konstanta silné interakce se vzdáleností roste. Na větších vzdálenostech lze závislost na předávané hybnosti popsat závislostí

${\displaystyle \alpha _{\mathrm {s} }(q)\approx {\frac {2\pi }{7\ln({\frac {q}{\Lambda _{\mathrm {QCD} }}})}}}$,

kde Λ_QCD je konstanta rozměru hybnosti s velikostí řádově 0,1 GeV/c.[5]

Důsledkem je, že při vzdalování vázaných kvarků způsobuje antistínění zhuštění siločar pole a jejich stažení do úzké trubice na spojnici a prudký nárůst přitažlivé síly, až dojde k energeticky výhodnější kreaci nového páru kvark-antikvark, který interakční trubici přeruší (vizte obrázek vpravo). Kvarky tak zůstávají uvězněny ve vázaných hadronových stavech (jako baryony s trojicí kvarků různého barevného náboje, nebo mezony s dvojicí kvark-antikvark dané barvy a odpovídající antibarvy). Není tedy teoreticky možná existence samostatného kvarku resp. obecněji samostatného nosiče barevného náboje – hovoří se o tzv. barevném uvěznění.

Naopak na velmi blízkých vzdálenostech se antistínění neprojevuje a kvarky se chovají jako volné, obklopené polem s Coulombovským potenciálem barevného náboje klesajícím nepřímo úměrně se vzdáleností – hovoří se o tzv. asymptotické svobodě kvarků.

Podobně jako u silné interakce převažuje u slabé interakce antistínění; protože počet kalibračních bosonů (3, konkrétně W⁺, W⁻, Z) je nižší (než 8 druhů gluonů), je tento vliv slabší. Konstanty elektromagnetické, slabé (resp. elektroslabé) a silné interakce se proto se snižující vzdáleností resp. s růstem předávané hybnosti sbližují.

Např. pro hybnost m_Zc (m_Z je klidová hmotnost intermediálního bosonu Z) odpovídající vzdálenosti řádově 10⁻¹⁹  m nabývají vazebné konstanty hodnot (v tradičním reciprokém vyjádření):[6][3]

• α_s(m_Zc) = 1/8,467(93)
• α₂(m_Zc) = α_g(m_Zc) = 1/29,5819(99) (příslušná poli intermediálních bosonů W)
• α_e(m_Zc) = 1/127,916(15).

Sbližování vazebných konstant je jedním ze základních kamenů tzv. teorie velkého sjednocení, podle které se při energiích řádově nad 10¹⁵ GeV sejdou obě konstanty elektroslabé interakce a konstanta silné interakce na společné hodnotě α_GU ≈ 1/40. Pro správný souběh do jedné hodnoty je nutné na základě teoretických úvah upravit vazebnou konstantu elektroslabé interakce příslušnou poli intermediálních bosonů Z (resp. B v elektroslabém sjednocení) koeficientem √(5/3), a navíc uvažovat existenci tzv. supersymetrie.[7][8][3]

Zatímco sbližování vazebných konstant s růstem předávané hybnosti bylo experimentálně potvrzeno, předpovědi teorie velkého sjednocení zatím zůstávají bez takovéhoto potvrzení; dosud např. nebyl pozorován předpovězený rozpad protonu. Nebyly ani nalezeny žádné částice, které by odpovídaly supesymetrickým partnerům stávajících elementárních částic látky a interakcí. Naopak, nejjednodušší teoretické modely velkého sjednocení již byly vyloučeny experimentálně zjištěnou hodnotou minimální doby života protonu.[3]