Čistě funkcionální

Jednoduché adresované seznamy jsou jako chleba a máslo datových struktur ve funkcionálních jazycích. V ML-odvozených jazycích a Haskellu, jsou čistě funkcionální protože jakmile je položka seznamu přiřazena nemůže být změněna, jenom zkopírována nebo zničena. Podívejte se na dva seznamy:

xs = [0, 1, 2]
ys = [3, 4, 5]

Ty by byly v paměti reprezentovány jako:

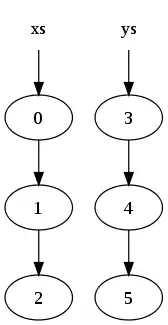
kde kolečko znamená položku v seznamu (šipka ven ukazuje další element seznamu a je to ukazatel na další položku seznamu). Zřetězením dvou seznamů:

zs = xs ++ ys

dostaneme následující strukturu paměti:

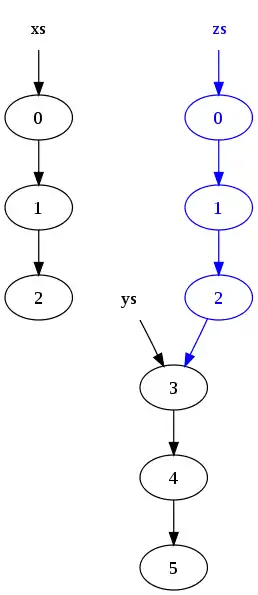
Všimněte si, že položky v seznamu xs byly zkopírovány, ale položky seznamu ys jsou sdíleny. Ve výsledku původní seznamy(xs a ys) přetrvávají a jsou nezměněny. Důvod ke kopírování je ten, že poslední položka v xs (která původně obsahuje dvojku) nemůže být změněna tak aby ukazovala na začátek ys, protože by to změnilo hodnotu xs.

Představte si binární strom, používaný pro rychlé hledání, ve kterém každá položka má rekurzivní invariantu, kde podpoložky vlevo jsou menší a podpoložky vpravo jsou větší. Například seznam:

xs = [a, b, c, d, f, g, h]

může být reprezentován následujícím binárním vyhledávacím stromem:

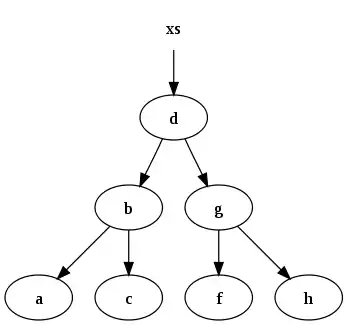
Funkce která vkládá data do binárního stromu a spravuje invarianty je:

fun insert (x, E) = T (E, x, E)
  | insert (x, s as T (a, y, b)) =
       if x < y then T (insert (x, a), y, b)
       else if x > y then T (a, y, insert (x, b))
       else s

Když provedeme

ys = insert ("e", xs)

dostaneme

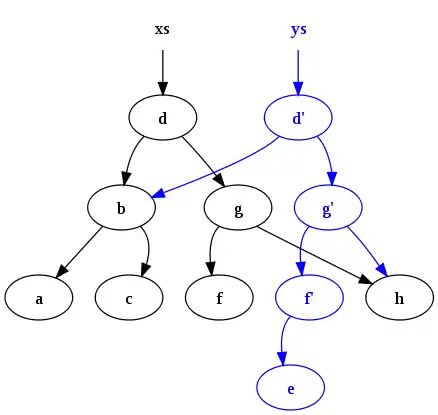
Všimněte si dvou věcí: 1. původní strom xs přetrvává. 2. spousta běžných položek je sdílena mezi novým a starým stromem. Takové přetrvávání a sdílení se těžko spravuje bez nějakého druhu garbage collection (GC), k automatickému uvolnění položek, které nemají žádnou živou referenci, a proto je GC obvykle součástí funkcionálních programovacích jazyků.

Přetrvávání čistě funkcionálních datových struktur může být výhodou ve vývoji spousty aplikací, které pracují s více verzemi objektů.

Například řekněme že máme slovník na webové stránce, která používá červeno-černý strom k ukládání jeho seznamů slov, která jsou synonymy a pro která slova jsou synonymy. Strom má kolem milionu položek. Nyní řekněme, že si přejeme přidat funkci, která dovoluje každému uživateli přidávat jejích vlastní slova do jejich osobních slovníků. Jedna cesta jak to udělat je kopírovat strom pro každého uživatele a poté do nich přidávat jejich vlastní slova, ale to je nevhodné, protože každý uživatel používající tuto službu by potřeboval paměť pro alespoň milion položek. Navíc by to způsobilo procesní zpoždění při kopírování stromu.

Lepší přístup je uložit slova v čistě funkcionálním červeno-černém stromu. Poté jednoduše vezmeme originální verzi a vytvoříme nový strom založený na tom základním pro každou sadu vlastních slov. Protože tyto nové stromy sdílí velkou část struktury s hlavním stromem, místo potřebné pro každého uživatele na nejvýše 2klog₂ n nebo zhruba 40 k položek, kde k reprezentuje počet vlastních slov.

Referenční průhlednost funkcionálních datových struktur rovněž usnadňuje analýzu a optimalizaci, a to formální i neformální.

Vzhledem k tomu, že každá hodnota v čistě funkcionálním výpočtu je vytvořena z existujících hodnot, zdá se nemožné vytvořit cyklus v referenčním grafu (graf který má hrany od objektů k objektům na který referují). Nicméně ve většině funkcionálních jazyků mohou být funkce definovány rekurzivně; tato možnost dovoluje strukturám použít funkcionální suspenzi. V líných jazycích jako je například Haskell jsou všechny datové struktury explicitně suspendovány; v těchto jazycích může být každá datová struktura rekurzivní. Některé jiné jazyky jako třeba Objective Caml, dovolují explicitní definici rekurzivních hodnot.

• Funkcionální programování
• Function-level programování

V tomto článku byl použit překlad textu z článku Purely functional na anglické Wikipedii.