Váhy (prístroj)

Vážením rozumieme obvykle porovnávanie tiaže telies (nemožno redukovať na gravitačnú silu - tiažové pole je totiž v sústavách spojených s povrchom Zeme superpozíciou gravitačnej sily a zotrvačnej odstredivej sily, spôsobené zemskou rotáciou) za účelom stanovenia hmotnosti. Tiažová sila je v danom mieste daná podľa 2. Newtonovho zákona súčinom hmotnosti a lokálne konštantného miestneho tiažového zrýchlenia. Rovnosť tiaže (pôsobiacej na záves váh) znamená teda aj rovnosť tiažovej sily (ktorou pôsobí tiažové pole na vážené telesá) a teda aj rovnosť ich hmotností. Účelom váženia je teda nájsť také závažie známej hmotnosti, ktoré bude mať rovnaký silový účinok na váhy ako skúmané teleso.

Pokiaľ je teda tiažové pôsobenie na dve telesá v danom mieste na povrchu Zeme rovnaké, hovoríme v bežnom živote, že majú rovnakú váhu a obvykle tým rozumieme, že majú rovnakú hmotnosť.

Pri veľmi presných váženiach sa však musí brať ohľad na ďalšie silové pôsobenia, ktoré sa nepodarilo odtieniť, napr. na vplyv aerostatického vztlaku - vztlaková sila podľa Archimedovho zákona pôsobí proti tiaži a znižuje tak silové pôsobenie na záves váh (redukcia na váženie vo vákuu). V prípade, že je namiesto závažia použité iné vyvažovacie silové pôsobenie, je nutné započítať aj premenlivosť lokálnej hodnoty tiažového zrýchlenia.

Kuchynské váhy (Francúzsko, 19. stor.)

Podľa konštrukcie a použitých fyzikálnych metód porovnávania sily F delíme váhy na radu typov, hlavne na:

• váhy pákové porovnávajú hmotnosť váženého predmetu so závažím o známej hmotnosti a ďalej sa delia na:
  • váhy rovnoramenné;
  • váhy nerovnoramenné;
  • váhy kyvadlové;
• váhy pružinové merajú pomocou deformácie pružiny;
• váhy tenzometrické merajú pomocou deformácie piezoelektrického prvku.

Súbor kuchynských závaží

Rovnoramenné váhy pracujú na princípe dvojramennej páky (vahadla) s rovnako dlhými ramenami. Na konci ramien bývajú zavesené misky, jedna na vážený predmet a druhá na závažie. Uprostred páky býva umiestnený jazýček, ktorý umožňuje presne odčítať, kedy sú obe strany v rovnováhe. Rovnoramenné pákové váhy sa líšia podľa toho, pre aký rozsah hmotností sú určené („váživosť“), aká sa vyžaduje citlivosť, presnosť a podobne. Rozlišujeme váhy analytické, lekárnické, kuchynské atď.

Súbor závaží (Mezopotámia) (Hematit, okolo 1700 pred Kr.)

Presnosť aj citlivosť váh vyžaduje, aby sa páka pohybovala pokiaľ možno bez trenia, preto býva uložená na ostriach, niekedy dokonca achátových a podobne. Citlivé váhy majú aretačné zariadenie, ktoré dovoľuje páku zdvihnúť z ostrí a znehybniť. Náročnejšie váženia sa robia v uzavretej skrinke, aby sa vylúčil vplyv prúdov vzduchu. Rovnoramenné pákové váhy sú jednoduché a pri dobre vyriešenom zavesení páky veľmi citlivé; nevýhodou je citlivosť na otrasy a potreba súboru závaží.

Sv. Michael váži duše (Dosková maľba. Soriguerola, Španielsko 13. stor.)

Rovnoramenné váhy patria k najstarším a už z predhistorických čias sú známe napríklad veľmi jemné váhy na drahokamy. Rovnoramenné váhy sú tiež symbolom spravodlivosti a už na staroegyptských reliéfoch sa vyskytuje motív váženia duší po smrti, veľmi rozšírený vo vrcholnom stredoveku v Európe. Na susednom obrázku archanjel Michal váži duše, ktoré mu druhý anjel podáva, a bráni ich proti diablom.

Decimálka

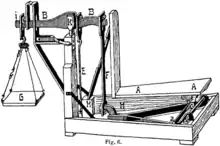
Tiež nerovnoramenné váhy pracujú na princípe dvojramennej páky, ale dĺžky oboch ramien sú rôzne. Toho možno využiť dvojakým spôsobom:

• Dĺžky oboch ramien môžu byť v pevnom pomere, napríklad 1:10. V tomto prípade bude vo vzťahu (1) platiť:

l₁ = 10.l₂

a váha bude v rovnováhe, keď bude hmotnosť závažia rovná jednej desatine hmotnosti váženého predmetu. Tak sú konštruované takzvané decimálky, váhy na objemný tovar napríklad v mechoch (obilie, zemiaky, uhlie atď.). Výhoda je v tom, že závažie nemusí byť tak ťažké a veľké. U decimálky je okrem toho „miska“ na tovar umiestená nízko, aby sa na ňu tovar ľahko nakladal. Dlhšie rameno páky je rozdelené na časť, ktorá je pod plošinou na tovar, a s vlastným vahadlom (B) je spojená zvislým tiahlom (F). Miesto jazýčku sa k indikácii používajú dva zobáčiky, ktoré sa v rovnováhe ocitnú proti sebe.

Na podobnom princípe avšak s väčším pomerom dĺžky ramien páky pracovali aj najstaršie typy tzv. mostových váh pre váženie povozov s nákladom a železničných vagónov, ktoré môžeme ešte dnes vidieť opustené na malých staniciach.

Rímska váha

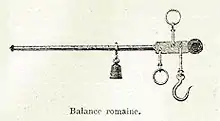
• Dĺžka jedného z ramien môže byť premenná; tak pracujú takzvané Rímske váhy. V tomto prípade stačí jediné závažie, ktoré sa posúva po dlhšom ramene páky tak dlho, až je váha v rovnováhe. Pre hmotnosť váženého tovaru potom platí vzťah (1), lenže hodnoty F₁ a l₂ sú konštantné, takže platí:

F₂ = k.l₁

a na ramene môže byť nanesená lineárna stupnica hmotností, resp „váh“. U osobných váh sa používa kombinácia dvoch posuvných závaží (napr. o hmotnosti 1 kg a 100 g) na dvoch paralelných ramenách, čo umožňuje presnejšie odčítanie.

Váha na dopisy

Kyvadlové váhy využívajú princíp vychýlenia ramena s pevným závažím zo zvislej polohy. Sila F₁, ktorou pôsobí kyvadlo o hmotnosti m₁ na konci páky je úmerná sínusu uhla α, ktorý kyvadlo zviera so zvislou osou podľa vzťahu.

F₁ = g. m₁.sin(α),

kde g je tiažové zrýchlenie. Vhodne voleným pákovým mechanizmom potom táto sila kompenzuje tiaž bremena F₂. Váhu možno priamo odčítať na kruhovej stupnici, ktorá však nie je lineárna; len pre malé hodnoty uhla α je hmotnosť váženého telesa priamo úmerná veľkosti tohto uhla. Typickým príkladom kyvadlových váh sú váhy na dopisy.

Pružinová váha

Pružinové váhy nepotrebujú závažie, ale využívajú Hookov zákon, podľa ktorého je veľkosť deformácie, napr. relatívneho predĺženia pružného materiálu Δl, priamo úmerné pôsobiacej sile F. Pružina, používaná u tohto typu váh môže byť buď špirálová, alebo valcová.

V prvom prípade sa pôsobením tiaže pružina skrúca a veľkosť skrútenia (uhol) sa odčíta na kruhovom ciferníku. Tento druh váhy sa používa napr. u lacnejších typov kuchynských váh alebo u váh na zásielky (listy).

V druhom prípade sa pružina preťahuje prípadne skracuje; táto zmena dĺžky sa indikuje na lineárnej stupnici. Tento typ váh sa dodnes často používa v poľnohospodárstve, napr. pre váženie mechov s obilím, zabitých zvierat alebo ich častí. Výhoda je v tom, že je prenosná a nepotrebuje závažie, nevýhodou je menšia citlivosť aj presnosť. Býva opatrená na jednom konci okom pre zavesenie na strop alebo inou konštrukciou, na druhom konci hákom pre zavesenie váženého predmetu.

Pozri aj: Silomer

Tenzometrické váhy určené predovšetkým pre použitie v laboratóriu

Váhy tenzometrické alebo tiež elektronické sú najmodernejším druhom váh. Sú založené podobne ako váhy pružinové na deformácii spôsobené tiažou váženého objektu. V tomto prípade sa však deformácia meria elektronickou cestou, väčšinou na základe piezoelektrického javu. Tieto váhy majú značnú presnosť a podľa konštrukcie, ktorá môže zahrňovať aj mechanické prevody, znižujúce veľkosť deformačnej sily, môžu mať aj veľký merací rozsah („váživosť“) od mikrogramov po desiatky ton, takže sa dajú používať ako v laboratóriách, tak pre váženie v kuchyni, v lekárskej ordinácii (osobné váhy) aj pre váženie vozidiel (mostové váhy, prenosné cestné váhy). Nezanedbateľnou výhodou elektronických váh je okolnosť, že môžu byť prepojené s počítačom, ktorý zaisťuje registráciu a ďalšie spracovanie nameraných hodnôt.

Pretože za dynamického stavu beztiaže nemožno uplatniť pre stanovovanie hmotnosti telies ich tiaže, boli vyvinuté pre potreby kozmonautiky špeciálne zariadenia, využívajúce zotrvačných vlastností hmoty plynúcich z 2. Newtonovho pohybového zákona. Teleso o celkovej hmotnosti m (napr. ľudské telo vrátane sedačky a ďalšej konštrukcie o presne známej hmotnosti) je upevnené pružinami, umožňujúcimi jeho kmitanie v jednom smere. Pretože sila, potrebná k pretiahnutiu alebo stlačeniu pružiny, je priamo úmerná predĺženiu pružiny x a súčasne rovná sile pôsobiacej opačným smerom a potrebnej k urýchleniu a telesa o hmotnosti m (pre zjednodušenie zanedbávame vlastnú hmotnosť pružinového systému), platí

m.a = m.(d²x/dt²) = -k.x,

kde koeficient k v sebe zahrňuje vlastnosti pružiny. Integráciou tejto diferenciálnej rovnice získame jej riešenie v tvare

x = A.sin(ω.t),

kde A je amplitúda kmitu (rozkmit), závisiaca na veľkosti počiatočného impulzu, t je čas a pre tzv. kruhovú frekvenciu ω platí

ω = 2π.f = (k / m)^1/2,

kde f je frekvencia kmitania systému. Z toho potom plynie

m = k / ( 4 π².f² ),

teda hmotnosť m je nepriamo úmerná štvorcu nameranej frekvencie kmitania.

Na palube Medzinárodnej vesmírnej stanice (ISS) je takéto zariadenie IMT-01 (Измеритель массы тела ИМТ-01) ruskej výroby používané k pravidelnej kontrole hmotnosti tiel kozmonautov.

• KOUŘIL, František; DUŠÁNEK, Jan. Váhy: jejich teorie a oprava. Mukačevo : [s.n.], 1938. 143 s., 26 tabuliek.

• Commons ponúka multimediálne súbory na tému Váhy (prístroj)

• Váženie (hmotnosť)
• Hmotnosť
• Váhy (znamenie)
• váha
• tiaž
• silomer

• HowStuffWorks:Inside a bathroom scale

Tento článok je čiastočný alebo úplný preklad článku Váhy na českej Wikipédii.