Brachistochrona
Brachistochrona (z gréckeho brachistos najkratší, chronos čas), označovaná tiež ako krivka najkratšieho spádu, je krivka spojujúca dva body, po ktorej sa hmotný bod dostane z počiatočného pokoja v jednom bode do druhého pôsobením homogénneho gravitačného poľa za najkratší čas.
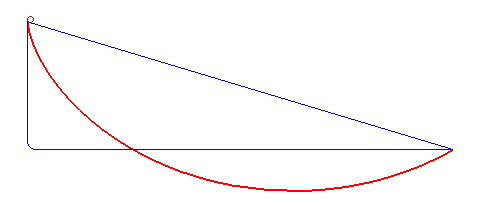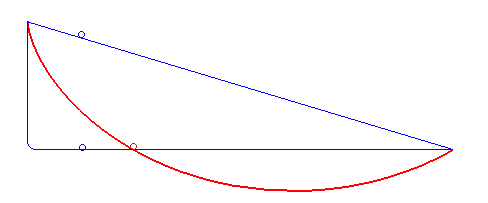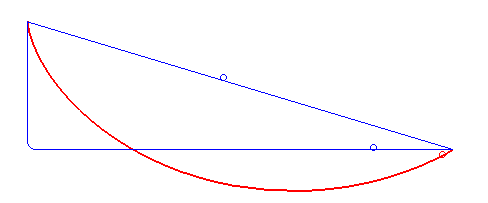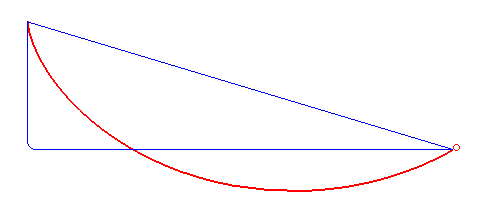
Názorné si je možné predstaviť, že hľadáme tvar drôtu, po ktorom sa má (bez trenia) kĺzať guľôčka medzi dvoma bodmi čo najrýchlejšie.
Pomocou pomerne zložitých postupov (vrátane variačného počtu) je možné dokázať, že brachistochrona je časť prostej cykloidy. Na rozdiel od klasickej polohy cykloidy používanej napr. u mostných oblúkov je však brachistochrona osovo prevrátená podľa vodorovnej osi.
Toto označenie zaviedol Johann Bernoulli v roku 1696 v časopise Acta Eruditorum a sám predložil riešenie (okrem svojho brata Jakoba a i.).
Úloha o brachistochrone
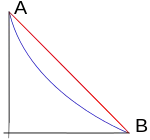
Úlohou je nájsť tvar spojnice dvoch bodov A a B, po ktorej by sa teleso pohybujúce sa vplyvom gravitačnej sily, dostalo z A do B v najkratšom čase. Predpokladá sa pohyb v homogénnom gravitačnom poli a odporové sily sa zanedbávajú. Pokiaľ by oba body ležali „pod sebou“ (na rovnakej zvislici), tak je zrejme úloha triviálna, hľadanou krivkou je úsečka.
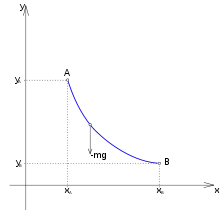
Úlohu je možné matematicky formulovať tak, že hľadáme takú hladku rovinnú krivku spojujúcu body (bez ujmy na všeobecnosti predpokladajme a ), po ktorej sa hmotný bod o hmotnosti pohybuje v tiažovom poli od bodu A do bodu B za najkratšiu dobu. Voľba súradnicového systému je zobrazená na obrázku, tiažová sila má obvyklý smer zápornej polosi y, vďaka symetrii pohyb nastáva v zvislej rovine obsahujúcej oba body.
Podľa zákona zachovania energie platí
- .
Úpravou tohoto vzťahu dostaneme výraz pre rýchlosť (ktorá zrejme nezávisí na hmotnosti),
- .
Pokiaľ predpokladáme rovnicu brachistochrony
- ,
rýchlosť je možne vyjadriť taktiež ako
- ,
kde bol použitý vzťah pre dráhu pohybu a fakt, že riešime len tú časť pohybu, kedy súradnica x rastie s časom.
Predpokladáme, že platí pre , vynechávame teda počiatočný bod a prípadnú hornú úvrať, pokiaľ by koncový bod ležal rovnako vysoko ako počiatočný. Pokiaľ teda predpokladáme , dostaneme z predchádzajúcich výrazov vzťah
Celkovú dobu potrebnú k prebehnutiu pozdĺž krivky z bodu A do B je možné zapísať ako
Fyzikálny problém sa teda redukuje na riešenie variačného problému minimalizácie funkcionálu s Lagrangeovou funkciou , nezávislou (explicitne) na x.
V tomto prípade existuje podľa Beltramiho identity pre príslušnú Eulerovo-Lagrangeovu diferenciálnu rovnicu extremály y prvý integrál v tvare
- .
Dosadením získame
- ,
kde je konštanta.
Úpravou posledného vzťahu dostaneme
Pretože , je možné označiť , čím získame
- .
Túto nelineárnu diferenciálnu rovnicu 1. rádu je možné výhodne riešiť substitúciou ,
riešením dostaneme parametrické vyjadrenie hľadanej krivky v tvare
- ,
- ,
kde sú integračné konštanty, ktorá sa určí z podmienky, že hľadaná krivka prechádza bodmi A a B.
Ide o časť prostej cykloidy, s úvraťou v bode A.
Iné odvodenie
Pretože ide o minimalizáciu doby pohybu, je možné úlohu o brachistochrone vyriešiť taktiež pomocou Fermatovho princípu z optiky, podľa ktorého je doba šírenia svetla extrémna. Celkovú dobu šírenia je možné vyjadriť
kde n je index lomu prostredia a c rýchlosť svetla vo vákuu.
Dráha minimalizujúca čas (extremála funkcionálu) je daná riešením rovnice, ktorá v nehomogénnom prostredí, kde rýchlosť svetla závisí len na jednej súradnici, má tvar (zákona lomu)
kde je odchýlka lúča od osi y. Po dosadení rýchlosti namiesto indexu lomu a za sínus (vlastne je to kosínus odchýlky od osi x, vyjadrený pomocou tangens – smernica dotyčnice dráhy), dostávame (značenie je rovnaké ako pri pôvodnom odvodení)
čo je rovnaká (diferenciálna) rovnica prostej cykloidy ako vyššie.
Vidíme, že brachistochrona je formálne geodetika plochy, kde vzdialenosť je daná koeficientmi prvej základnej formy
Literatúra
- Rektorys, K. a spol.: Přehled užité matematiky I.. Prometheus, Praha, 2003, 7. vydanie. ISBN 80-7196-179-5
- Brdička M., Hladík A. : Teoretická mechanika. Academia, Praha, 1987.
- BRDIČKA, Miroslav. Brachystochrona či brachistochrona?. Pokroky matematiky, fyziky a astronomie, 1972, roč. 17, čís. 4, s. 204. Dostupné online. ISSN 0032-2423.
Pozri aj
Zdroj
- Tento článok je čiastočný alebo úplný preklad článku Brachistochrona na českej Wikipédii.