Zpětná vazba

Pohled zavádějící pojem zpětné vazby vznikl ve dvacátých letech 20. století v počátcích elektroniky (r. 1906 vynález elektronky, Lee de Forest) a na ni navazující sdělovací techniky. Pak se rozšířil do povědomí široké veřejnosti a začal díky lidové tvořivosti získávat různé významy, mnohdy opouštějící ten původní. Je však nutno si uvědomovat mez mezi původním významem a tím nezávazným, lidovým. Tak je třeba nepoužívat ten lidový, pokud se má vysvětlit nějaký děj, odehrávající se třeba v elektronickém zařízení, jinak vznikají nesmysly.

Příklad použití zpětné vazby v audionovém stupni rozhlasového přijimače

Ve sdělovací technice se pojem zpětné vazby vyvinul proto, že se objevily nežádoucí (nestabilita zesilovače) i revolučně žádoucí vlivy (např. razantně snížit výstupní impedanci zesilovače, snížit jeho zkreslení) zpětného působení, které zpětná vazba znázorňuje – modeluje. První patent týkající se zpětné vazby ale byl zaregistrován až v roce 1932, kdy Harold Stephen Black patentoval zesilovač s pevným zesílením. V dvacátých letech 20. století byl totiž problém s tím, že zesílení bylo silně závislé na frekvenci zesilovaného signálu. Tuto vadu odstranil Blackův zesilovač použitím zpětné vazby. Proslýchá se^[zdroj?], že myšlenka zpětné vazby ho napadla při sobotní ranní procházce na mostě přes řeku Hudson (1927).

Obrázek 1 : Patent na zesilovač

Zpočátku samozřejmě nebyla zpětná vazba vnímána vědci a techniky takto precizně – abstraktně, ale jako technický poznatek, výsledek pozorování, měření a úsudku. Na abstraktní úroveň se začínal přesouvat, až když bylo třeba pouhá pozorování a experimenty, vyztužit krokem poznání, a to nebylo možné jinak, než použitím matematického popisu. Vnikla tak teorie zpětné vazby, bez které by aplikace nebyly možné, experimenty při znalosti teorie mohou být mnohem zasvěcenější a rychleji postupující k cíli. Vyvinula se i grafická symbolika modulů znázorňující ideu zpětné vazby, používající trojúhelníky znázorňující směr pohybu sledovaného rozruchu, někdy místo nich používají obdélníky se šipkami na spojnicích mezi uvedenými zobrazeními modulů. Moduly mají vstup (někdy i několik) a jeden výstup, tak jsou jednosměrné, říká se jim unilatelární. Schémata používající unilatelární moduly se nazývají blokové schéma (někdy nazývané Blackův diagram), zde níže obr. 2 a obr. 3., nebo jako grafy signálových toků [2], [3], [4].

Krok ze světa interakcí (elektronických obvodů) k unilatelárnímu modelu zpětné vazby, v němž jsou na obr. 2. a 3. uvedené moduly A a B, znamená odvození jejich matematického popisu. Každá změna v realizaci modulů (změna vnitřního zapojení a hodnot komponentů elektronického obvodu) si vyžaduje znovu určit matematický popis modulů, a moduly se navíc vzájemně ovlivňují interakcemi. Byla proto zvolena schůdnější cesta, a to vytvoření unilatelárních modulů. Je to realizace toho, co se vyskytuje ve schématu zpětné vazby. Schéma může být mnohem složitěji, než v obr. 2. a 3., ty ukazují jen princip. Vytvoření unilatelárních modulů je zajištěno jejich speciální konstrukcí a přísunem vnější energie, říká se jim aktivní členy. Příkladem jsou moduly informačních, sdělovacích a regulačních soustav (např. lineární operační zesilovače, logické obvody počítačů, hydraulické a pneumatické zesilovače v automatickém řízení a neurony biologického mozku: axony jsou výstupy, dendrity jsou vstupy). Princip je ten, že výstupy (díky přísunu vnější energie modulu) disponují takovou energetickou rezervou, že vstupy následujících modulů na onen vstup napojené, nijak hodnoty toho výstupu neovlivňují. Vniká tak stavebnice se snadnou výměnou modulů, a pro každý modul je znám jeho matematický popis, tedy jeho vlastnosti. Určení matematického popisu soustavy unilatelárních modulů je pak mnohem snadnější (slouží k tomu algebra bokových schémat, uvedená např. v: [5], [6]), než kdyby se pracovalo s elektrickým obvodem, v němž se odehrávají interakce. Tak hlavní úsilí může být soustředěno na návrh a odladění celku, jímž může být sdělovací zařízení nebo třeba soustava automatického řízení, apod.

Jinou obdobou unilatelárních modulů jsou jejich počítačové modely. Např. v oboru automatického řízení se používají programy modelující soustavu automatického řízení, tak, jako by byla k dispozici stavebnice unilatelárních modulů. Takovým programům se říká blokově orientované.

Postupně, někdy jako pohled proti proudu času, lidé začali odhalovat, že zpětná vazba je k rozeznání i jinde. Příkladem může být Wattův odstředivý regulátor, který byl původně vymyšlen ad hoc., ze znalosti toho, jak jedna součástka mechanicky postrkuje jinou (z hlediska fyziky mezi nimi probíhají interakce a pohyb součástek je jejich výsledkem), takže pokud se otáčky nežádaně zvyšují, odstředivá síla tlačí závaží na rotujícím věnci od středu a tak i nahoru, a ventil přívodu páry se přivírá a obráceně. Zpětná vazba se uzavírá přes parní stroj, který změnou otáček reaguje na změnu přívodu páry, a tak mění otáčky. Parní stroj je ve schématu (obr. 2. a 3.) symbolizován modulem A, regulátor symbolem B. Zpětná vazba se ukázala být významným principem automatického řízení. Byly odhalovány zpětné vazby v mnoha přírodních jevech, včetně procesů v lidském těle. Americký vědec Mason[3], přišel s nápadem, že bude pomocí grafů zobrazovat jednosměrné akce a reakce, získané aktem poznání s použitím Ohmova zákona a Kirchhoffových zákonů v elektrických RLC obvodech. Ukazuje, že jednosměrné akce a reakce tvoří zpětnovazební smyčky modelující původní interakce. Grafy nazval grafy signálových toků, a ty se v propracovanější formě s úspěchem stále používají[4].

Zmapování zpětných vazeb ve světě interakcí se obecně děje tak, že během aktu poznání (viz Věda) jsou interakce rozloženy (použitím zákona akce a reakce) na jednosměrně působící akce a reakce, které můžeme chápat jako zpětné vazby. Tak je aktem poznání svět interakcí převeden na svět (jednosměrně – od někud někam tekoucí) informace, někdy se používá pojem signálové toky. Takto získaný informační (matematicky reprezentovaný kognitivní) model lze graficky znázornit unilaterálními bloky, a zpětné vazby popisující akce a reakce původních interakcí, jsou mezi moduly patrné. Řadu příkladů lze nalézt v [7], [8]. Použití unilatelárních schémat, umožňující různé interpretace, od sledování toků hmotných a energetických rozruchů po sledování toku informace orientuje zpětnou vazbu do kybernetiky.

Při použití metod zjišťování, jak zpětná vazba ovlivňuje vlastnosti dané soustavy modulů, se uzavřená smyčka pomyslně (nebo v realitě skutečně) rozpojí. Zjišťují se vlastnosti takto rozpojené smyčky (moduly A a B jsou v sérii), a z nich se dají zjistit vlastnosti smyčky uzavřené, např. stabilita. Používají se i metody, kdy se uvažují vlastnosti soustavy bez větve zaváděné zpětné vazby, a odděleně vlastnosti samotné větve zpětné vazby, a z nich se stanoví vlastnosti soustavy s uzavřenou zpětnou vazbou. Jednoduché příklady jsou uvedeny níže na obrázcích 2. a 3.

Pokud zvýšení hodnoty, přiváděné z výstupu na vstup, způsobí další zvýšení hodnoty na výstupu, jedná se o kladnou zpětnou vazbu. Pokud je navíc výsledné zesílení celého cyklu větší než 1, může výstupní hodnota systému nekontrolovatelně růst. Obvykle tento růst samozřejmě narazí na omezení daná charakterem systému, v němž vazba probíhá.

Obrázek 2: Kladná zpětná vazba

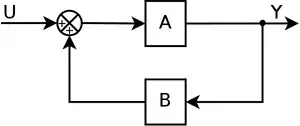
Kladná zpětná vazba se obvykle využívá k zesílení nebo k akceleraci žádoucích jevů.

Matematicky je přenos kladné zpětné vazby popsán následujícími rovnicemi.

${\displaystyle Y(s)=A\cdot U(s)+B\cdot A\cdot Y(s)}$

${\displaystyle {\frac {Y(s)}{U(s)}}={\frac {A}{1-B\cdot A}}}$

Pokud zvýšení hodnoty, přiváděné z výstupu na vstup, způsobí snížení hodnoty na výstupu, jedná se o zápornou zpětnou vazbu. Tento druh vazby se využívá v regulační technice pro udržení stálých parametrů systémů, neboť v případě výskytu výchylky od ustáleného stavu dokáže zpětná vazba působit proti této výchylce a potlačit ji.

Obrázek 3: Záporná zpětná vazba

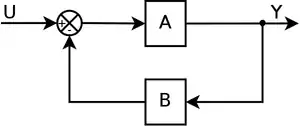
V přenosu se oproti kladné zpětné vazbě pouze změní znaménko ve jmenovateli.

${\displaystyle Y(s)=A\cdot U(s)-B\cdot A\cdot Y(s)}$

${\displaystyle {\frac {Y(s)}{U(s)}}={\frac {A}{1+B\cdot A}}}$

Z podstaty toho, že výstup procesu, který je ovlivněn zpětnou vazbou, působí v každé iteraci na jeho vstup, naznačuje, že celkový stav zpětnovazební veličiny se bude zvyšovat nebo snižovat geometrickou řadou, čili bude mít exponenciální průběh.

Zpětná vazba (feedback) má velkou roli v systémové dynamice, je to jedna ze základních relací mezi entitami a veličinami systémů, které moduluje. Zpoždění mezi obdržením zpětnovazebních informací může být stěžejní v strategii řízení těch nejdůležitějších procesů a demografických či ekonomických ukazatelů (počet obyvatel, hmotná úroveň jednotlivce, objem obchodu, …) v rámci regionu, státu nebo i v globálním měřítku (logistických řetězcích, systémech a cyklech) [9] .