Věta o hybnosti proudu kapaliny
Věta o hybnostech proudu kapaliny je jedním ze základních zákonů hydrodynamiky. Je přizpůsobením impulsové věty mechaniky hmotného bodu pro ustálený proud kapaliny. Uvažuje se jen účinek na omezený výsek proudu, přičemž není nutné znát ani podrobnosti proudění, ani ztráty v daném úseku, avšak musíme znát všechny vnější síly, které na kapalinu v tomto výseku proudu působí.
Věta o hybnosti
Suma vnějších sil se rovná změně hybnosti kapaliny[1],
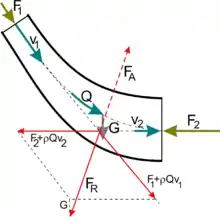
kde [kgm−3] je hustota kapaliny, [m3s−1] objemový průtok, a vektory rychlosti ve vstupním a výstupním profilu a
kde a [N] jsou vektory síly působící na vstupní a výstupní profil (zpravidla síly tlakové, kde [Pa] je tlak a [m2] průtočná plocha daného profilu), [N] tíha kapaliny uzavřené mezi vstupním a výstupním profilem a [N] síla, kterou působí stěna vedení proudu na objem kapaliny mezi vstupním a výstupním profilem.
Ve většině případů nás však spíše zajímá silový účinek proudu na stěny, kterými je veden, nebo na plochy, na něž dopadá. V těchto případech pak místo síly , kterou působí stěna na proud, uvažujeme její reakci .
Aplikace věty o hybnosti
Výpočet v souřadném systému
Zaveďme kartézský souřadný systém; osa x směřuje zleva doprava, osa y shora dolů. Potom výpočet provedeme ve složkách jednotlivých dílčích sil:
kde úhly a jsou úhly, které svírá síla a , resp. osa proudu v profilu 1 a 2 se souřadnicovými osami.
Celková síla , kterou proud působí na své vedení, je pak
a tato výsledná síla svírá s osou x souřadného systému úhel , který snadno určíme ze vztahu
.
Pokud je tíha vody ve srovnání s ostatními silami malá, lze ji zanedbat. Pokud zkoumaný segment proudu leží v horizontální rovině, tíha kapaliny působí kolmo k této rovině i všem ostatním členům rovnice a ve výpočtu se tudíž neuplatňuje, a při návrhu konstrukce je nutné ji uvažovat samostatně.
Účinek paprsku na těleso či plochu
V těchto případech se obvykle předpokládá symetrické obtékání tělesa či plochy a tíha kapaliny se zpravidla zanedbává. Protože při obtékání tělesa či plochy vznikají ztráty jednak třením paprsku na tělese či ploše, jednak ohybem proudnic a tvorbou vírů při nárazu paprsku na těleso, redukuje se teoretická hodnota výsledné síly korekčním součinitelem .
Když paprsek osově dopadá na kužel o vrcholovém úhlu postavený vrcholem proti paprsku, paprsek se symetricky rozdělí po plášti tohoto kuželu. Protože vzdálenost vrcholu a odtokové hrany (či délka povrchové přímky) obvykle není velká, lze zhruba uvažovat a výsledná reakce tedy bude
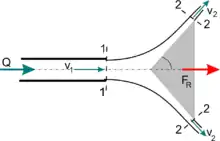
,
po převodu do kartézského souřadného systému s osou x rovnoběžnou s osou paprsku
a po zavedení výše zmíněného korekčního součinitele
.
V případě kruhové desky je a tedy . Při dostatečném rozměru desky ( kde [m] je průměr desky a [m] průměr paprsku) a vzdálenosti [m] desky od výtokového otvoru lze uvažovat hodnotu redukčního součinitele .
Maximální možnou sílu dostaneme, pokud paprsek dopadá do středu plochy tvaru duté polokoule. Potom dojde k tomu, že vektor rychlosti směřuje proti směru paprsku a tedy čili a výsledná síla bude
kde redukční součinitel .
Účinek paprsku na pohybující se plochu
Pokud se plocha, na kterou parsek dopadá, pohybuje ve směru vektoru rychlosti rychlostí [ms−1], dopadá paprsek na tuto plochu relativní rychlostí [ms−1], kterou použijeme pro výpočet síly namísto rychlosti paprsku . Podobně i průtok je nutné uvažovat jako průtok relativní kde [m2] je průtočná plocha výtokového otvoru (resp. průtočná plocha v paprsku).
Pro soustavu lopatek nebo kanálů (např. oběžné kolo Peltonovy turbiny), otáčejících se kolem pevné osy obvodovou rychlostí [ms−1] uvažujeme při výpočtu síly opět relativní rychlost , avšak průtok bereme jako .
Reference
- Boor, B., Kunštátský, J. a Patočka, C. (1968): Hydraulika pro vodohospodářské stavby. SNTL/Alfa Praha/Bratislava