Symetrická diference

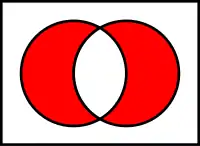
V matematice se jako symetrická diference nebo symetrický rozdíl dvou množin označuje taková množina, která obsahuje všechny prvky z obou množin, které nejsou v jejich průniku. Symetrická diference množin A a B se značí jako

A\,\triangle \,B

Vennův diagram pro

A\triangle B,

Symetrický rozdíl množin je
Sjednocení bez průsečíku množin

~\setminus ~

~=~

nebo

A\div B

nebo

A\ominus B.

Například symetrická diference množin $\{1,2,3\}$ a $\{3,4\}$ je množina $\{1,2,4\}$ . Symetrická diference množin dívek a studentů je množina všech dívek, které nejsou studentky, a všech chlapců studentů.

Potenční množina libovolné množiny s operací symetrické diference je abelovou grupou; neutrální prvek grupy je prázdná množina, a protože symetrická diference množiny se sebou samou je prázdná množina, tak každý prvek potenční množiny je svým vlastním inverzním prvkem.

Vlastnosti

Vennův diagram pro

A\triangle B\triangle C

~\triangle ~

~=~

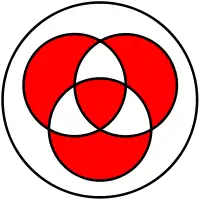
Symetrická diference je ekvivalentní se sjednocením obou rozdílů množin:

A\,\triangle \,B=(A\smallsetminus B)\cup (B\smallsetminus A)

a také může být vyjádřena jako sjednocení dvou množin bez jejich průniku:

A\,\triangle \,B=(A\cup B)\smallsetminus (A\cap B)

nebo pomocí operace XOR:

A\,\triangle \,B=\{x:(x\in A)\oplus (x\in B)\}.

Zvláště pak platí, že:

A\triangle B\subseteq A\cup B.

Symetrická diference je komutativní a asociativní:

A\,\triangle \,B=B\,\triangle \,A,\,

(A\,\triangle \,B)\,\triangle \,C=A\,\triangle \,(B\,\triangle \,C).\,

Průnik je distributivní nad symetrickou diferencí:

A\cap (B\,\triangle \,C)=(A\cap B)\,\triangle \,(A\cap C),

Reference

V tomto článku byl použit překlad textu z článku Symmetric difference na anglické Wikipedii.

Externí odkazy

Obrázky, zvuky či videa k tématu symetrická diference na Wikimedia Commons

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.