Simulované žíhání
Simulované žíhání (simulované ochlazování, anglicky Simulated annealing, SA) je pravděpodobnostní optimalizační metoda prohledávání stavového prostoru založená na simulaci žíhání oceli. Při prohledávání stavového prostoru se může snadno stát, že algoritmus uvázne v lokálním minimu. V metodě se tomu snažíme zabránit tím, že provádíme i změny k horšímu, velké hlavně zpočátku, a díky tomu se můžeme dostat z lokálního minima. Velikost změny záleží na teplotě. Čím větší je teplota, tím větší se provádí změny. Algoritmus pracuje pouze s jedním kandidátním řešením. Obyčejný gradientní algoritmus přijímá nové řešení, pouze pokud je lepší než řešení stávající. Při simulovaném žíhání jsou s určitou pravděpodobností přijímána i řešení horší. Pravděpodobnost přijetí i horšího řešení je přímo závislá na teplotě a nepřímo na velikosti zhoršení. V průběhu výpočtu algoritmu je teplota postupně snižována na základě rychlosti konvergence (přibližování se cíli). Pokud algoritmus konverguje rychle (hodnocení stavů rychle klesá), snižuje se teplota také rychle a algoritmu je tak bráněno pokračovat do hůře hodnoceného stavu. Konverguje-li algoritmus pomalu (hodnocení stavů moc neklesá), zpomalí se snižování teploty, aby se případně podařilo vyprostit z lokálního minima.
Pokud nejsme spokojeni s výsledkem, tak teplotu lze i zvyšovat. Potom pravděpodobnost, že bude algoritmus pokračovat do hůře hodnoceného stavu také stoupá, jestliže se algoritmu nedaří (neustálým pokračováním do co nejlépe hodnocených stavů) přibližovat se cíli.
Algoritmus nezaručuje nalezení globálního minima. Pro zlepšení výsledků algoritmus můžeme pustit několikrát z různých, například náhodných, počátečních stavů.
Přehled
Termodynamický stav některých fyzikálních systémů a funkce E(s), která má být minimalizována, je analogická s vnitřní energií systému v tomto stavu. Cílem je převést systém z libovolného "počátečního stavu“ do stavu s minimální možnou energií.
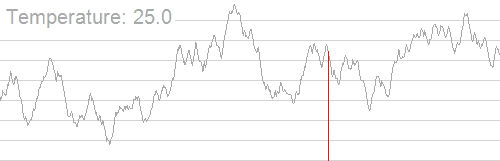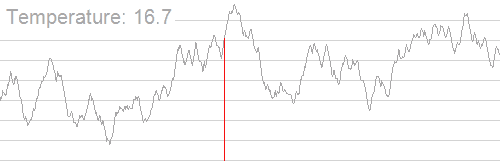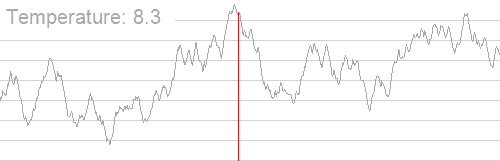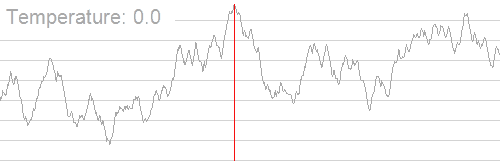
Základní iterace
V každém kroku simulovaná žíhací heuristika bere v úvahu některý sousední stav současného stavu a spojenec se rozhoduje mezi přesunem systému do stavu ve stavu "s“. Tyto pravděpodobnostní nakonec vedou systém k přechodu do stavu s nižší energií. Tento krok se obvykle opakuje, dokud systém nedosáhne stavu, který je pro aplikaci dostatečně dobrý, nebo dokud není vyčerpán daný výpočetní rozpočet.
Sousedé stavu
Optimalizace řešení zahrnuje problému hodnocení stavů sousedů, což jsou nové stavy produkované konzervativní změnou daného stavu. Například v problému obchodního cestujícího je každý stav obvykle definován jako permutace měst, která mají být navštívena, a sousedé jakéhokoli stavu jsou množinou permutací vytvořených prohozením jakýchkoli dvou z těchto měst. Dobře definovaný způsob, jakým jsou stavy prohazovány, aby vytvářely sousední stavy, se nazývá "tah“ a různé pohyby poskytují různé sady sousedních stavů. Tyto kroky obvykle vedou k minimálním změnám posledního stavu, ve snaze o postupné vylepšování řešení iterativním vylepšováním jeho částí (například městská spojení v problému obchodního cestujícího).
Jednoduché heuristické typy jako gradientní algoritmus, které se pohybují hledáním lepšího souseda za lepším sousedem a zastaví se, když dosáhnou řešení, které nemá lepší sousedy, nemohou zaručit, že povedou k některému ze stávajících lepší řešení jejich výsledkem může být jednoduše jen lokální optimum, zatímco nejlepším řešením by bylo globální optimum, které by se mohlo lišit. Metaheuristiky používají sousedy řešení jako způsob, jak prozkoumat prostor řešení, a přestože dávají přednost lepším sousedům, přijímají také horší sousedy, aby se vyhnuli uvíznutí v místních optimech; mohou najít globální optimum, pokud běží dostatečně dlouho.
Pravděpodobnosti přijetí
Pravděpodobnost uskutečnění změny stavu z aktuálního stavu do kandidátního nového stavu je určena potvrzením pravděpodobnostní funkce , která závisí na energiích a obou stavů a na globálním časově proměnném parametru , který se nazývá "teplota“. Stavy s menší energií jsou lepší než stavy s vyšší energií. Pravděpodobnostní funkce musí být kladná, i když je větší než . Tato funkce brání tomu, aby se metoda zasekla na místním minimu, které je horší než globální.
Když má tendenci k nule, pravděpodobnost musí mít tendenci k nule pokud a v opačném případě na kladnou hodnotu. U dostatečně malých hodnot pak systém bude stále více upřednostňovat pohyby, které vedou "z kopce“ (tj. K nižším energetickým hodnotám), a vyhnout se těm, které jdou "do kopce“. U se postup redukuje na Hladový algoritmus, který dělá pouze přechody z kopce.
V původním popisu simulovaného žíhání byla pravděpodobnost rovna 1, když ,neboli procedůra se vždy, pokud mohla, pohnula z kopce, bez ohledu na teplotu. Mnoho popisů a implementací simulovaného žíhání stále bere tuto podmínku jako součást definice metody. Tato podmínka není pro fungování metody nezbytná.
Funkce se obvykle volí tak, aby se pravděpodobnost přijetí tahu snížila, když rozdíl se zvyšuje, neboli malé pohyby do kopce jsou pravděpodobnější než velké. Tento požadavek však není nezbytně nutný, pokud jsou splněny výše uvedené požadavky.
Vzhledem k těmto vlastnostem hraje teplota rozhodující roli při řízení vývoje stavu systému s ohledem na jeho citlivost na variace energií systému. Přesněji řečeno, u velkého je vývoj citlivý na hrubší variace energie, zatímco je citlivý na jemnější variace energie, když je malý.
Plán žíhání


Název a inspirace algoritmu vyžadují zajímavou vlastnost související s kolísáním teploty, která má být vložena do provozních charakteristik algoritmu. To vyžaduje postupné snižování teploty v průběhu simulace. Algoritmus začíná zpočátku nastaveným na vysokou hodnotu (nebo nekonečno) a poté se v každém kroku snižuje po nějakém "žíhacím plánu“, který může uživatel určit, ale musí končít na na konci přiděleného časového rozpočtu. Tímto způsobem se očekává, že se systém bude pohybovat zpočátku směrem k široké oblasti vyhledávacího prostoru obsahující dobré řešení, ignorující malé rysy energetické funkce; pak směřovat k nízkoenergetickým regionům, které se zužují a zužují; a nakonec se pohybovat z kopce podle heuristiky gradientního sestupu.
Pro jakýkoli daný konečný problém se pravděpodobnost, že simulovaný algoritmus žíhání končí řešením globalní optimum, blíží 1, protože se rozvrh žíhání prodlužuje. [1] This theoretical result, however, is not particularly helpful, since the time required to ensure a significant probability of success will usually exceed the time required for a řešení hrubou silou of the prostorů řešení.
Pseudokód
Následující pseudokód představuje simulovanou žíhací heuristiku, jak je popsáno výše. Začíná to od stavu s0 a pokračuje až do maximálně kmax kroků. V tomto procesu by volání Soused('s')) mělo generovat náhodně vybraného souseda daného státu s; volání Random(0,1) by mělo vybrat a vrátit hodnotu v rozsahu [0,1], rovnoměrného rozdělení. Časový plán žíhání je definován voláním teplota(r), které by mělo vrátit použitou teplotu, s ohledem na zlomek r časového rozpočtu, který byl zatím vyčerpán.
Výběr parametrů
Aby bylo možné použít metodu simulovaného žíhání na konkrétní problém, je třeba zadat následující parametry: stavový prostor, energetickou (cílovou) funkci E(), postup generátoru kandidáta soused(), funkce pravděpodobnosti přijetí P() a plán žíhání teplota() A počáteční teplota <počáteční teplota>. Tyto volby mohou mít významný dopad na efektivitu metody. Bohužel neexistují žádné volby těchto parametrů, které by byly dobré pro všechny problémy, a neexistuje žádný obecný způsob, jak najít nejlepší možnosti pro daný problém. V následujících částech je uvedeno několik obecných pokynů.
Dostatečně blízko souseda
Simulované žíhání lze modelovat jako náhodný průchod po vyhledávacím grafu, jehož vrcholy jsou všechny možné stavy a jejichž hrany jsou kandidátní pohyby. Základním požadavkem na funkci Neighbor() je, že musí na tomto grafu poskytovat dostatečně krátkou cestu od počátečního stavu do jakéhokoli stavu, který může být globálním optimem průměr hledání graf musí být malý. Ve výše uvedeném příkladu obchodního cestujícího má například vyhledávací prostor pro měst (2,4 kvintilionu) stavů; počet sousedů každého vrcholu je hran a průměr grafu je .
Pravděpodobnosti přechodu
Pro zkoumání chování simulovaného žíhání u konkrétního problému může být užitečné vzít v úvahu "pravděpodobnosti přechodu“, které vyplývají z různých konstrukčních možností provedených při implementaci algoritmu. Pro každou hranu vyhledávacího grafu je pravděpodobnost přechodu definována jako pravděpodobnost, že se simulovaný žíhací algoritmus přesune do stavu , když je jeho aktuální stav . Tato pravděpodobnost závisí na aktuální teplotě zadané funkcí teplota(), na pořadí, ve kterém se pohyby kandidátů generují pomocí funkce Neighbor(), a na funkci pravděpodobnosti přijetí P(). (Všimněte si, že pravděpodobnost přechodu není "jednoduše“ , protože kandidáti jsou testováni sériově.)
Pravděpodobnosti přijetí
Specifikace Neighbor(), P() a temperature() je částečně nadbytečná. V praxi je běžné použít pro mnoho problémů stejnou funkci přijetí P() a upravit další dvě funkce podle konkrétního problému.
Metoda formulovaná Kirkpatrick et al. Byla funkce pravděpodobnosti přijetí <(e,e',T) definována jako 1, pokud a jinak. Tento vzorec byl povrchně ospravedlněn analogií s přechody fyzikálního systému; odpovídá Metropolisův–Hastingsův algoritmus, v případě, že a návrhové rozdělení Metropolis–Hastings je symetrické. Tato pravděpodobnost přijetí se však často používá pro simulované žíhání, i když funkce Neighbor(), která je analogická distribuci návrhů v Metropolis–Hastings, není symetrická nebo vůbec není pravděpodobná. Výsledkem je, že pravděpodobnosti přechodu algoritmu simulovaného žíhání neodpovídají přechodům analogického fyzikálního systému a dlouhodobé rozdělení stavů při konstantní teplotě nemusí být nijak podobné distribuci termodynamické rovnováhy ve stavech fyzikálního systému při jakékoli teplotě. Většina popisů simulovaného žíhání nicméně předpokládá původní akceptační funkci, která je pravděpodobně zakódována v mnoha implementacích SA.
Roku 1990, Moscato and Fontanari [2] and independently Dueck and Scheuer,[3] navrhl, aby deterministická aktualizace (tj. ta, která není založena na pravidlu pravděpodobnosti přijetí), mohla urychlit proces optimalizace, aniž by to mělo dopad na konečnou kvalitu. Moscato a Fontanari docházejí k závěru z pozorování analogie křivky "měrného tepla“ žíhání "aktualizace prahové hodnoty“ pocházející z jejich studie, že „stochasticita aktualizace Metropolis v simulovaném žíhacím algoritmu nehraje při hledání blízké -optimální minima ". Místo toho navrhli, že „vyhlazení prostředí nákladové funkce při vysoké teplotě a postupné definování minim během procesu chlazení jsou základními ingrediencemi pro úspěch simulovaného žíhání.“ Metoda se následně popularizovala pod označením "akceptování prahu“ kvůli Dueckově a Scheuerově označení. V roce 2001 Franz, Hoffmann a Salamon ukázali, že deterministická aktualizační strategie je skutečně optimální v rámci velké třídy algoritmů, které simulují náhodnou procházku po prostředí nákladů a energie. [4]
Efektivní generování kandidátů
Při výběru kandidátního generátoru Neighbor() je třeba vzít v úvahu, že po několika iteracích simulovaného žíhacího algoritmu se očekává, že aktuální stav bude mít mnohem nižší energii než náhodný stav. Obecně by tedy měl být generátor vychýlen směrem k kandidátským pohybům, kde je pravděpodobné, že energie cílového stavu bude podobná energii aktuálního stavu. Tento heuristický (což je hlavní princip [[[Metropolis–Hastingsův algoritmus]])] má tendenci vylučovat "velmi dobré“ pohyby kandidátů i "velmi špatné“; první možnost je však obvykle mnohem méně častá než druhá, takže heuristika má obecně dobrou učínnost.
U výše uvedeného problému obchodního cestujícího se například očekává, že výměna dvou „po sobě jdoucích“ měst v průchodu s nízkou energií bude mít mírný vliv na jeho energii (délku); vzhledem k tomu, že výměna dvou "libovolných“ měst je mnohem pravděpodobnější, že prodlouží jejich délku, než ji zkrátí. Očekává se tedy, že sousední generátor prohožení bude fungovat lépe než generátor libovolného prohození, i když by tento mohl poskytnout poněkud kratší cestu k optimálnímu (s prohozením namísto ).
Přesnější výrok heuristiky je, že je třeba vyzkoušet první kandidátské stavy , pro které je . Pro "standardní“ akceptační funkci výše to znamená, že je v řádu nebo méně. Ve výše uvedeném příkladu obchodního cestujícího by tedy bylo možné použít funkci Neighbor(), která prohodí dvě náhodná města, kde pravděpodobnost výběru dvojice měst zmizí, jak se jejich vzdálenost zvětší za .
Vyhýbání se překážkám
Při výběru kandidátního generátoru Neighbor() je také nutné pokusit se snížit počet "hlubokých“ místních minimálních stavů(nebo sad spojených stavů), které mají mnohem nižší energii než všechny sousední stavy. Takové "uzavřené údolí“ energetické funkce mohou zachytit simulovaný žíhací algoritmus s vysokou pravděpodobností (zhruba úměrný počtu stavů v údolí) a po velmi dlouhou dobu (zhruba exponenciální na energetický rozdíl mezi okolnímy stavy a dnem údolí).
Je zpravidla nemožné navrhnout generátor kandidátů, který splní tento cíl a také upřednostní kandidáty s podobnou energií. Na druhou stranu lze často výrazně zlepšit účinnost simulovaného žíhání pomocí relativně jednoduchých změn v generátoru. Například v problému obchodního cestujícího není těžké vytvořit dva průchody , s téměř stejnou délkou tak, že (1) je optimální, (2) každá sekvence prohození párů stavů, která převádí na , prochází průchody, které jsou mnohem delší než obě, a (3) lze převést na převrácením (obrácením pořadí) sady po sobě jdoucích stavů. V tomto příkladu leží a v různých "údolí“, pokud generátor provádí pouze náhodné výměny párů; ale budou ve stejném údolí, pokud generátor provede náhodné převrácení segmentu.
Plán chlazení
Fyzikální analogie, která se používá k ospravedlnění simulovaného žíhání, předpokládá, že rychlost ochlazování je dostatečně nízká na to, aby rozdělení pravděpodobnosti současného stavu bylo vždy blízko termodynamické rovnováze. Bohužel relaxační doba, po které musí člověk po změně teploty čekat na obnovení rovnováhy silně závisí na „topografii“ energetické funkce a na aktuální teplotě. V simulovaném žíhacím algoritmu závisí doba relaxace také na kandidátním generátoru, a to velmi komplikovaným způsobem. Všimněte si, že všechny tyto parametry jsou obvykle poskytovány jako černá skříňka simulovanému žíhacímu algoritmu. Ideální rychlost chlazení proto nelze určit předem a měla by být empiricky upravena pro každý problém. Algoritmus Adaptivní simulované žíhání řeší tento problém připojením plánu chlazení k postupu hledání. Další adaptivní přístup jako termodynamické simulované žíhání, [5] automaticky upravuje teplotu v každém kroku na základě rozdílu energie mezi těmito dvěma stavy podle zákonů termodynamiky.
Reference
- GRANVILLE, V.; KRIVANEK, M.; RASSON, J.-P. Simulated annealing: A proof of convergence. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1994, s. 652–656. DOI 10.1109/34.295910. (anglicky)
- MOSCATO, P.; FONTANARI, J.F. Stochastic versus deterministic update in simulated annealing. Physics Letters A. 1990, s. 204–208. DOI 10.1016/0375-9601(90)90166-L. (anglicky)
- DUECK, G.; SCHEUER, T. Threshold accepting: A general purpose optimization algorithm appearing superior to simulated annealing. Journal of Computational Physics. 1990, s. 161–175. ISSN 0021-9991. DOI 10.1016/0021-9991(90)90201-B. (anglicky)
- FRANZ, A.; HOFFMANN, K.H.; SALAMON, P. Best optimal strategy for finding ground states. Physical Review Letters. 2001, s. 5219–5222. DOI 10.1103/PhysRevLett.86.5219. PMID 11384462. (anglicky)
- DE VICENTE, Juan; LANCHARES, Juan; HERMIDA, Román. Placement by thermodynamic simulated annealing. Physics Letters A. 2003, s. 415–423. DOI 10.1016/j.physleta.2003.08.070. Bibcode 2003PhLA..317..415D. (anglicky)