Sférické harmonické funkce

Sloupce: l=0 do 4
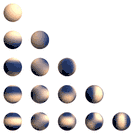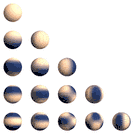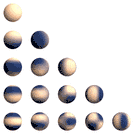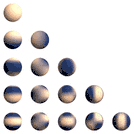
Řádky: m=0 do ±4
Dvě neimaginární sférické harmoniky, které jsou lineární kombinací Y_l,m a Y_l,-m jsou shodné, ale navzájem otočené o 90 stupňů kolem osy z.

Laplaceova rovnice ve sférických souřadnicích je:

${\displaystyle {1 \over r^{2}}{\partial \over \partial r}\left(r^{2}{\partial f \over \partial r}\right)+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\partial f \over \partial \theta }\right)+{1 \over r^{2}\sin ^{2}\theta }{\partial ^{2}f \over \partial \varphi ^{2}}=0}$

(viz sférická soustava souřadnic).

Separace proměnných vede k řešení vyjádřitelnému v goniometických funkcích a Legendrových polynomech.

Obecné řešení, které je konečné s r jdoucím k nekonečnu je lineární kombinací funkcí ve tvaru

${\displaystyle r^{-1-\ell }\cos(m\varphi )P_{\ell }^{m}(\cos {\theta })}$

a

${\displaystyle r^{-1-\ell }\sin(m\varphi )P_{\ell }^{m}(\cos {\theta })}$

kde ${\displaystyle P_{\ell }^{m}}$ jsou přidružené Legendrovy polynomy s celočíselnými parametry ${\displaystyle \ell \geq 0}$ a m od 0 do ${\displaystyle \ell }$.

Jinými slovy řešení s celočíselnými parametry ${\displaystyle \ell \geq 0}$ a m od ${\displaystyle -\ell }$ do ${\displaystyle \ell }$ lze psát jako lineární kombinaci:

${\displaystyle U_{\ell ,m}(r,\theta ,\varphi )=r^{-1-\ell }Y_{\ell }^{m}(\theta ,\varphi )}$

kde funkce Y jsou sférické harmonické funkce s parametry l, m, které lze psát jako:

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )={\sqrt {{(2\ell +1) \over 4\pi }{(\ell -m)! \over (\ell +m)!}}}\cdot e^{im\varphi }\cdot P_{\ell }^{m}(\cos {\theta })}$

Sférické harmoniky splňují normalizační podmínku (δ_aa = 1 a δ_ab = 0 pokud a ≠ b)

${\displaystyle \int _{\theta =0}^{\pi }\int _{\varphi =0}^{2\pi }Y_{\ell }^{m}Y_{\ell '}^{m'*}\,\mathrm {d} \Omega =\delta _{\ell \ell '}\delta _{mm'},\quad \quad \mathrm {d} \Omega =\sin \theta \,\mathrm {d} \varphi \,\mathrm {d} \theta }$

platí pro ně

${\displaystyle Y_{\ell }^{-m}(\theta ,\varphi )=\left(-1\right)^{m}Y_{\ell }^{m*}(\theta ,\varphi )}$

a splňují relace úplnosti

${\displaystyle \sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }Y_{\ell }^{m}(\theta ,\varphi )Y_{\ell }^{m*}(\theta ',\varphi ')=\delta \left(\cos \theta -\cos \theta '\right)\delta \left(\varphi -\varphi '\right),}$

kde δ(x) je Diracova delta funkce.

Y1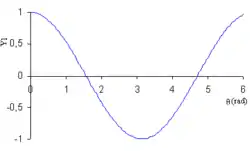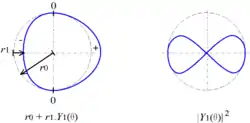
Y2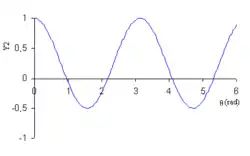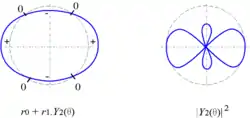
Y3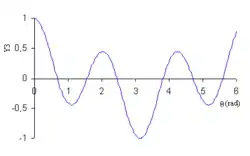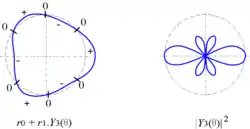

Alternativní sadu sférických harmonik bez imaginární části získáme jako

${\displaystyle Y_{\ell }^{0}\quad \quad {\mbox{ pro }}\ 0\leq \ell \leq \infty }$

a

${\displaystyle {1 \over {\sqrt {2}}}\left((-1)^{m}Y_{\ell }^{m}+Y_{\ell }^{-m}\right)\quad \quad {\mbox{ pro }}\ 0\leq \ell \leq \infty ,\ 1\leq m\leq \ell }$

a

${\displaystyle {1 \over i{\sqrt {2}}}\left((-1)^{m}Y_{\ell }^{m}-Y_{\ell }^{-m}\right)\quad \quad {\mbox{ pro }}\ 0\leq \ell \leq \infty ,\ 1\leq m\leq \ell }$

Sférické harmoniky vyjádřené v kartézských souřadnicích vyjádříme dosazením

${\displaystyle \cos \theta ={z \over r},\qquad e^{\pm ni\varphi }\cdot \sin ^{n}\theta ={(x\pm iy)^{n} \over r^{n}},\qquad r={\sqrt {x^{2}+y^{2}+z^{2}}}}$.

Zde jsou první sférické harmoniky:

${\displaystyle Y_{0}^{0}(\theta ,\varphi )={1 \over 2}{\sqrt {1 \over \pi }}}$

${\displaystyle Y_{1}^{-1}(x)={1 \over 2}{\sqrt {3 \over 2\pi }}\cdot e^{-i\varphi }\cdot \sin \theta \quad ={1 \over 2}{\sqrt {3 \over 2\pi }}\cdot {(x-iy) \over r}}$

${\displaystyle Y_{1}^{0}(x)={1 \over 2}{\sqrt {3 \over \pi }}\cdot \cos \theta \quad ={1 \over 2}{\sqrt {3 \over \pi }}\cdot {z \over r}}$

${\displaystyle Y_{1}^{1}(x)={-1 \over 2}{\sqrt {3 \over 2\pi }}\cdot e^{i\varphi }\cdot \sin \theta \quad ={-1 \over 2}{\sqrt {3 \over 2\pi }}\cdot {(x+iy) \over r}}$

${\displaystyle Y_{2}^{-2}(\theta ,\varphi )={1 \over 4}{\sqrt {15 \over 2\pi }}\cdot e^{-2i\varphi }\cdot \sin ^{2}\theta }$

${\displaystyle Y_{2}^{-1}(\theta ,\varphi )={1 \over 2}{\sqrt {15 \over 2\pi }}\cdot e^{-i\varphi }\cdot \sin \theta \cdot \cos \theta }$

${\displaystyle Y_{2}^{0}(\theta ,\varphi )={1 \over 4}{\sqrt {5 \over \pi }}\cdot (3\cos ^{2}\theta -1)}$

${\displaystyle Y_{2}^{1}(\theta ,\varphi )={-1 \over 2}{\sqrt {15 \over 2\pi }}\cdot e^{i\varphi }\cdot \sin \theta \cdot \cos \theta }$

${\displaystyle Y_{2}^{2}(\theta ,\varphi )={1 \over 4}{\sqrt {15 \over 2\pi }}\cdot e^{2i\varphi }\cdot \sin ^{2}\theta }$

${\displaystyle Y_{3}^{0}(\theta ,\varphi )={1 \over 4}{\sqrt {7 \over \pi }}\cdot (5\cos ^{3}\theta -3\cos \theta )}$

Tabulka sférických harmonických funkcí

• Obrázky, zvuky či videa k tématu Sférické harmonické funkce na Wikimedia Commons