Schwenkova věta

Není těžké dokázat, že když platí podmínka číslo jedna, je uzavřená procházka jezdce nemožná.

Představme si typickou šachovnici střídající černá a bílá pole. Kdykoliv se jezdec pohne, skončí vždy na poli opačné barvy. Pokud tedy stojí na bílém poli, následujícím skokem se ocitne na poli černém. Pokud stojí na černém, skočí na bílé. Proto při uzavřené procházce navštíví jezdec stejný počet bílých a černých polí.

Protože ale obě čísla m a n jsou lichá, je počet polí šachovnice rovněž lichý a tedy počet bílých a černých polí na šachovnici je nutně odlišný (například šachovnice 5 × 5 má 13 polí jedné barvy a 12 druhé).

Má-li jezdec dokončit uzavřenou procházku, musí navštívit stejný počet bílých a černých polí, ovšem uvažovaná šachovnice má odlišný počet bílých a černých polí, proto na ní uzavřenou procházku nelze dokončit. Mohou však existovat řešení otevřená.

Podmínka č. 2 říká, že má-li kratší strana délku 1, 2 nebo 4, potom není uzavřená procházka možná.

Na první pohled je jasné, že pokud m = 1 nebo 2, není jezdcova procházka vůbec možná: jezdec není schopen navštívit každé pole této šachovnice (s výjimkou triviálního případu „šachovnice“ 1 × 1 pole).

Lze však také prokázat, že uzavřená procházka nemá řešení ani na šachovnici o 4 × n polích.

Předpokládejme, že úloha má na šachovnici 4 × n řešení. Sestavme 2 množiny polí ${\displaystyle A_{1}}$ a ${\displaystyle B_{1}}$, přičemž ${\displaystyle A_{1}}$ bude obsahovat jednu polovinu polí šachovnice (např. bílá pole) a ${\displaystyle B_{1}}$ druhou (např. černá pole). Jak již bylo uvedeno výše, jezdec musí při svém pohybu střídat bílá a černá pole (${\displaystyle A_{1}}$ a ${\displaystyle B_{1}}$).

Jezdec musí střídat zelená a červená pole

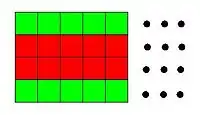
Na diagramu vpravo můžeme definovat ${\displaystyle A_{2}}$ jako množinu zelených polí a ${\displaystyle B_{2}}$ jako množinu červených polí. Počty zelených a červených polí si jsou rovny. Je zřejmé, že z pole v ${\displaystyle A_{2}}$ musí jezdec v dalším tahu skočit na pole v ${\displaystyle B_{2}}$. A protože musí navštívit každé pole, musí z pole v množině ${\displaystyle B_{2}}$ skočit na pole množiny ${\displaystyle A_{2}}$ (pokud by po sobě následovaly dva tahy v rámci množiny ${\displaystyle B_{2}}$, musely by po sobě následovat také dva tahy v rámci množiny ${\displaystyle A_{2}}$, což není možné).

Zde však dochází k rozporu:

1. Řekněme, že první pole, které jezdec navštíví, bude pole z množiny ${\displaystyle A_{1}}$ a současně z množiny ${\displaystyle A_{2}}$. Pokud tomu tak není, přehodíme označení množin ${\displaystyle A_{1}}$ a ${\displaystyle B_{1}}$ a případně ${\displaystyle A_{2}}$ a ${\displaystyle B_{2}}$ tak, aby to byla pravda.
2. Druhé navštívené pole musí být potom prvkem množin ${\displaystyle B_{1}}$ a ${\displaystyle B_{2}}$.
3. Třetí navštívené pole musí být prvkem množin ${\displaystyle A_{1}}$ a ${\displaystyle A_{2}}$.
4. Čtvrté navštívené pole musí být prvkem množin ${\displaystyle B_{1}}$ a ${\displaystyle B_{2}}$.
5. A tak dále.

Z toho plyne, že množina ${\displaystyle A_{1}}$ má stejné prvky jako množina ${\displaystyle A_{2}}$ a že množina ${\displaystyle B_{1}}$ má stejné prvky jako množina ${\displaystyle B_{2}}$. To však evidentně není pravda, neboť červeno-zelený vzor na diagramu neodpovídá černo-bílému šachovnicovému vzoru; množina červených polí není stejná jako množina černých polí (a množina zelených není stejná jako množina bílých).

Z toho plyne, že výše uvedený předpoklad byl nepravdivý a na šachovnici 4 × n nelze pro žádné n nalézt řešení jezdcovy procházky.

Neexistenci uzavřeného řešení v případě podmínky č. 3 lze prokázat rozborem případů.

K důkazu věty je nutné prokázat ještě opačnou implikaci, tj. že na všech obdélníkových šachovnicích, které nespadají do jedné ze tří výše uvedených kategorií, lze uzavřené řešení jezdcovy procházky nalézt.