Rozdělení chí kvadrát
Rozdělení chí kvadrát čili rozdělení (jinak také Pearsonovo rozdělení) s stupni volnosti je spojité rozdělení pravděpodobnosti, které je často využíváno ve statistice. Velký význam má pro určování, zda množina dat vyhovuje dané distribuční funkci.
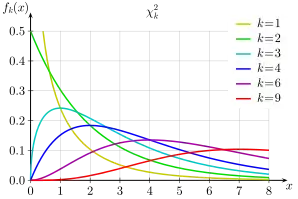
Rozdělení o stupních volnosti, které se označuje , je rozdělení náhodné veličiny , kde je vzájemně nezávislých náhodných veličin s normovaným normálním rozdělením .
Rozdělení má hustotu pravděpodobnosti
Charakteristiky rozdělení
Střední hodnota rozdělení je
Rozdělení má rozptyl
Momentová vytvořující funkce pro rozdělení má tvar
Tabulka některých kvantilů pro některé počty stupňů volnosti:
| stupňů volnosti | q0,95 | q0,99 |
|---|---|---|
| 1 | 3,84 | 6,63 |
| 2 | 5,99 | 9,21 |
| 3 | 7,81 | 11,34 |
| 4 | 9,49 | 13,28 |
| 5 | 11,07 | 15,09 |
| 10 | 18,31 | 23,21 |
| 15 | 25,00 | 30,58 |
| 20 | 31,41 | 37,57 |
| 30 | 43,77 | 50,89 |
| 40 | 55,76 | 63,69 |
| 50 | 67,50 | 76,15 |
| N velké (>100) |
Poznámka: 95% kvantil odpovídá kritické hodnotě pro 5% hladinu významnosti, 99% kvantil kritické hodnotě pro 1% hladinu významnosti.
Vlastnosti
Rozdělení se s rostoucím blíží k normálnímu rozdělení se střední hodnotou a rozptylem .