Mealyho automat
V informatice se pojmem Mealyho stroj označuje konečný automat s výstupem. Výstup je generován na základě příchozího vstupu i momentálního stavu, ve kterém se automat nachází. To znamená, že stavový diagram automatu má ke každému přechodu přiřazenu nejen vstupní hodnotu, kterou je přechod aktivován, ale i výstupní hodnotu, která je při aktivaci přechodu vygenerována. Tímto Mealyho automat připomíná synchronní komunikaci: Nejen že reaguje na hranu vstupního signálu, ale jakmile ho zpracuje a dosáhne dalšího stavu, jednou vygeneruje výstupní hodnotu, puls výstupního signálu, a pak už žádný výstup neposkytuje; zase až do další vstupní hodnoty předložené ke zpracování. Totiž nejen, že jsou stavy Mealyho stroje podmnožinou kartézského součinu množiny (předešlých) stavů a vstupní abecedy, ale i jeho výstupy jsou podmnožinou kartézského součinu stavů a výstupní abecedy.
Mealyho stroje jsou obdobou Mooreových strojů, u těch ale výstup nezáleží na současném vstupu, a proto mají Mooreovy stroje vždy zpoždění. Ovšem z pohledu realizované logické funkce je každý Mealyho stroj ekvivalentní nějakému Moorově stroji.[zdroj?] Na rozdíl od Mealyho automatů jsou Moorovy automaty schopny trvale poskytovat hodnotu svého vnitřního stavu, zpřístupněnou výstupem. Výstupy Moorových automatů jsou přímo kopií jeho stavů, bez kartézského součinu.
Formální definice
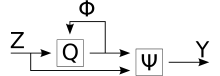
Mealyho stroj je uspořádaná šestice , kde:
- Z = {z1, z2, ... ,zn} - konečná vstupní abeceda
- Q = {q1, q2, ... ,qn} - neprázdná konečná množina stavů proměnlivých v čase
- Y = {y1, y2, ... ,yn) - konečná výstupní abeceda
- Φ = q(t+1) = Φ[q(t), z(t)] - přechodová funkce
- Ψ = y(t) = Ψ[q(t), z(t)] - výstupní funkce, záleží na stavu, ve kterém se automat nachází a zároveň i na vstupním signálu
- q - počáteční stav z množiny Q
nebo podle jiné terminologie (S, Σ, Λ, T, G, s0), kde
- Q = S je neprázdná konečná množina stavů
- Z = Σ je konečná vstupní abeceda
- Y = Λ je konečná výstupní abeceda
- Φ = T je přechodová funkce (T : S × Σ → S)
- Ψ = G je výstupní funkce (G : S × Σ → Λ)
- q = s0 ∈ S je počáteční stav.
V definici může být použita i sedmice: sedmým parametrem by pak byla množina koncových stavů.
Příklad s diagramem
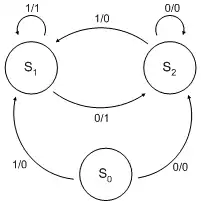
Automat je popsán svým přechodovým diagramem:
- Tento stroj generuje výstup bez zpoždění.
- Pro vstupy x0x1…xn vygeneruje sekvenci 0y0y1…yn-1.
- S0, S1 a S2 jsou stavy.
- S0 je počáteční stav.
- Každá hrana přechodu je nadepsána "j / k", kde j je přijatý vstup a k je vygenerovaný výstup. Samotným stavům pak nejsou žádné hodnoty určeny. Výstup automatu, závislý na vstupech, je pak dán až aktivací odchozího přechodu.
Jiný příklad s tabulkami
Mealy
Automat má tabulkou definovanou svou přechodovou funkci a jednu výstupní funkci:
| stav | vstup z | stav | výstup y | |||
|---|---|---|---|---|---|---|
| 0 | 1 | yz=0 | yz=1 | |||
| A | C | B | A | 0 | 0 | |
| B | C | A | B | 1 | 0 | |
| C | A | C | C | 1 | 0 | |
Převod Mealy → Moore
Rozšíření počtu stavů:
- Každý Mealyho stav se rozdvojí, protože každý Mooreho stav může mít dvě hodnoty. Stejně se rozdvojí i jeho odchozí přechody, počet hran se tak až zdvojnásobí.
- Hodnota v Mooreho stavu je dána požadovanou výstupní hodnotou, obrácená úvaha.
Celkový počet výstupních hodnot se nezmění: zde se ze tří Mealyho stavů generujících každý dvě výstupní hodnoty stane šest Mooreho stavů, kde každý generuje právě jednu výstupní hodnotu.
| stav | vstup z | hodnota q výstup y | |
|---|---|---|---|
| 0 | 1 | ||
| (A,0) | (C,0) | (B,0) | 0 |
| (A,1) | (C,0) | (B,0) | 1 |
| (B,0) | (C,1) | (A,0) | 0 |
| (B,1) | (C,1) | (A,0) | 1 |
| (C,0) | (A,1) | (C,0) | 0 |
| (C,1) | (A,1) | (C,0) | 1 |
Vyškrtání nedosažitelných stavů: Zde stav (B,1) není cílem ani jednoho z 12 přechodů, takže je nedosažitelný. Tento stav by ale stále mohl mít význam jako počáteční: Sice se nedá dostat do něj, ale dá se dostat z něj.
Odkazy
Literatura
- Doc. Ing. Jiří Bayer, CSc; Dr.Ing. Zdeněk Hanzálek; Ing. Richard Šusta: Logické systémy pro řízení, Vydavatelství ČVUT, Fakulta elektrotechnická, Praha, 2000, ISBN 80-01-02147-5, dce.felk.cvut.cz
- Doc. Ing. Jaromír Kolouch, CSc., Programovatelné logické obvody a hradlová pole, 6.1 Transformace stavového automatu Moorova typu na Mealyho typ a naopak, řešení grantového projektu FRVŠ - tematický okruh F1, specifikace d; feec.vutbr.cz