Měrná energie profilu

Mějme otevřené koryto obecného tvaru a sledujme, jak se při konstantním průtoku ${\displaystyle Q}$ [m³s⁻¹] bude se změnou polohy hladiny (resp. hloubky proudu) měnit měrná energie proudění v daném profilu.

Energie proudění ${\displaystyle E}$ (zde vyjádřená jako energetická výška v metrech) je rovna (viz např. [1], [2])

${\displaystyle E={y+{{\alpha v^{2}} \over {2g}}}=y+{{\alpha Q^{2}} \over {2gS^{2}}}}$

kde ${\displaystyle y}$ [m] je hloubka vody, resp. výška hladiny nad nejnižším bodem dna, ${\displaystyle \alpha }$ Coriolisovo číslo, ${\displaystyle v}$ [ms⁻¹] střední průřezová rychlost, ${\displaystyle g}$ [ms⁻²] gravitační zrychlení a ${\displaystyle S}$ [m²] průtočná plocha.

Je zřejmé, že pokud se hloubka ${\displaystyle y}$ bude blížit nule, poroste střední průřezová rychlost a tedy i energie nade všechny meze. Obdobně pokud průtočná plocha ${\displaystyle S}$ poroste nade všechny meze, bude se velikost energie blížit hloubce proudění. Pokud tuto závislost, která je pro dané koryto, resp. tvar profilu a daný průtok jedinečná, vyneseme do grafu

Měrná energie profilu

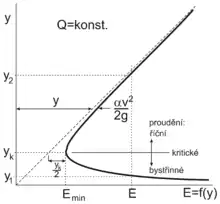
, bude grafem funkce ${\displaystyle E=f(y)}$ křivka, jejíž jednou asymptotou je tedy osa ${\displaystyle x\backsim E}$, druhou asymptotou pak přímka ${\displaystyle E=y}$. Křivka má dále minimum pro jistou hodnotu hloubky ${\displaystyle y_{k}}$ (tzv. kritickou hloubku). Tato kritická hloubka je jednak rozhraním mezi pohybem říčním (čili podkritickým) pro hloubky ${\displaystyle y>y_{k}}$ a pohybem bystřinným (čili nadkritickým) pro hloubky ${\displaystyle y<y_{k}}$, jednak hloubkou samostatného režimu proudění, tzv. proudění či pohybu kritického (${\displaystyle y=y_{k}}$). Při kritickém pohybu tedy proudění prochází daným profilem s minimem energie.

Metodami matematické analýzy lze minimum funkce dané výše uvedenou energetickou rovnicí snadno vyřešit, čímž získáme tzv. obecnou podmínku kritického pohybu

${\displaystyle {{\alpha Q^{2}B_{k}} \over {gS_{k}^{3}}}=1}$, často též uváděnou ve tvaru ${\displaystyle {{\alpha Q^{2}} \over g}={{S_{k}^{3}} \over {B_{k}}}}$,

z níž lze kritickou hloubku ${\displaystyle y_{k}}$ poměrně snadno určit. Ve výše uvedených vztazích ${\displaystyle B}$ [m] je šířka koryta v hladině a index ${\displaystyle k}$ značí hodnotu dané veličiny při právě kritické hloubce ${\displaystyle y_{k}}$. Obecná podmínka kritického pohledu je analyticky řešitelná pouze pro několik málo speciálních případů, pro obecné koryto (a již i pro koryto tvaru lichoběžníku) je nutné ji řešit numerickými metodami, případně graficko-početně.

Též lze pro obdélníkový profil odvodit, že minimum energie ${\displaystyle E_{min}=1,5y_{k}}$, čili rychlostní výška kritického pohybu je v tomto případě právě rovna polovině kritické hloubky; pro obecný profil je rychlostní výška kritického pohybu právě rovna polovině střední hloubky (definici viz níže)[1].

Pokud potřebujeme znát pouze typ proudění a nikoliv kritickou hloubku, bývá pro určení typu proudění jednodušší použít Froudeho čísla, v tomto případě udávaného jako

${\displaystyle Fr={v \over \surd {gh_{s}}}}$

kde ${\displaystyle h_{s}}$ [m] je střední hloubka, ${\displaystyle h_{s}=S/B}$.

Potom pokud:

${\displaystyle Fr<1}$ proudění je říční,

${\displaystyle Fr=1}$ proudění je kritické,

${\displaystyle Fr>1}$ proudění je bystřinné.

V přírodě se setkáváme převážně s prouděním říčním, proudění bystřinné se např. i v horských bystřinách za běžných okolností vyskytuje jen lokálně, globálně bývá proudění říční.

Bystřinné proudění je charakterizováno vysokými rychlostmi, z nich vyplývá řada nepříznivých jevů - zvýšené namáhání koryta, velké převýšení hladiny v obloucích, tvorba stojatých příčných vln při změně směru či změně profilu koryta, provzdušení vodního proudu vedoucí ke zvětšení hloubky, při přechodu bystřinného proudění do proudění říčního tvorba vodního skoku (a tím další namáhání dna), za určitých podmínek i tvorba translačních vln atp. Všechny tyto jevy jsou ve vodohospodářské praxi nevítané a vyžadují zvláštní přístupy a opatření (viz [3]).

Proudění kritické a kritickému blízké (též zvané okolokritické) je též velmi specifickým problémem a vyznačuje se zejména nestabilitami, navíc je velmi málo probádáno a při návrhu koryta je nejlépe se této oblasti pokud možno vyhnout