Kvaternionová grupa

Kvaternionová grupa $Q_{8}$ je konečná nekomutativní grupa řádu 8, spolu s dihedrální grupou (symetrie čtverce) $D_{4}$ jediná taková. Lze ji definovat pomocí jednotkových kvaternionů s operací kvaternionového násobení, jako množinu $Q_{8}=\{1,-1,i,-i,j,-j,k,-k\}$ .

Graf cyklů kvaternionové grupy

Q_{8}

. Každá barva specifikuje sérii mocnin nějakého prvku. Například červená znázorňuje cyklus i ² = −1, i ³ = −i a i ⁴ = 1.

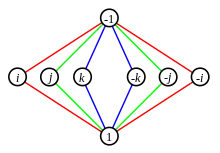
Grupa má reprezentaci

Q_{8}=\langle -1,i,j,k\mid (-1)^{2}=1,\;i^{2}=j^{2}=k^{2}=ijk=-1\rangle ,\,\!

kde $1$ je neutrální prvek grupy a $-1$ komutuje se všemi dalšími prvky.

Násobení prvků podmnožiny $\{\pm i,\pm j,\pm k\}$ se chová stejně jako vektorový součin vektorů ortonormální báze třírozměrného Eukleidovského prostoru:

{\begin{alignedat}{2}ij&=k,&\qquad ji&=-k,\\jk&=i,&kj&=-i,\\ki&=j,&ik&=-j.\end{alignedat}}

Maticová reprezentace

Kvaternionovou grupu lze reprezentovat komplexními maticemi $2\times 2$ zobrazením

1\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}}

i\mapsto {\begin{pmatrix}i&0\\0&-i\end{pmatrix}}

j\mapsto {\begin{pmatrix}0&1\\-1&0\end{pmatrix}}

k\mapsto {\begin{pmatrix}0&i\\i&0\end{pmatrix}}

a $-1,-i,-j,-k$ jsou reprezentovány maticemi s opačnými znaménky všech koeficientů. Součiny těchto matic splňují výše uvedené grupové rovnosti. Všechny tyto matice jsou unitární, jedná se tedy o unitární reprezentaci grupy $Q_{8}$ na dvourozměrném komplexním prostoru.

Reference

V tomto článku byl použit překlad textu z článku Quaternion group na anglické Wikipedii.

Externí odkazy

Obrázky, zvuky či videa k tématu kvaternionová grupa na Wikimedia Commons

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.