Jednotkový hydrogram

Povodí je jako celek považováno za systém, ve kterém se srážkový vstup (efektivní déšť) transformuje na výstup v podobě přímého odtoku. Transformační funkcí je jednotkový hydrogram (anglicky unit hydrograph, zkratka UH), který se definuje jako hydrogram přímého odtoku vyvolaný efektivním deštěm o jednotkovém objemu, o stálé intenzitě a rovnoměrně rozloženém na povodí, za předpokladu platnosti principu superpozice a principu časové invariance.

Podle principu superpozice závisí velikost výstupu lineárně na velikosti vstupu, časové rozložení výstupu není velikostí vstupu ovlivněno. Výsledný výstup je roven součtu výstupů vyvolaných jednotlivými vstupy.

Princip časové invariance zaručuje, že se vstupy lišící se vzájemně pouze časem svého počátku transformují do výstupů, které se od sebe liší také pouze časem svého počátku. Čas počátku vstupu nemá vliv na velikost ani časové rozložení výstupu.

Jednotkový hydrogram, který je vyvolaný efektivním deštěm o době trvání D, se nazývá jednotkový hydrogram pro déšť doby trvání D nebo také D-hodinový jednotkový hydrogram (zkratka TUH). Aby byly splněny podmínky stálé intenzity efektivního deště a jeho jednotkového objemu, musí být intenzita efektivního deště rovna 1/D.

Příklad jednotkového hydrogramu pro déšť doby trvání D

Pokud je efektivní déšť s proměnlivou intenzitou a libovolným objemem rozdělen do časových intervalů délky Δτ, ve kterých má intenzitu konstantní, a je-li znám TUH pro dobu trvání deště Δτ, lze s využitím principů určit přímý odtok, který je tímto deštěm vyvolán.

Díky principu superpozice se zjistí velikost odtoku pro efektivní déšť o jiném než jednotkovém objemu P_ef ≠ 1. Při objemu 1 a intenzitě 1/Δτ je velikost odtoku v jednotkovém hydrogramu u(t), při objemu P_ef a intenzitě I je velikost odtoku v témže čase Q(t)=u(t).I.Δτ = u(t).P_ef. Princip časové invariance zaručuje, že jednotkový hydrogram pro dobu trvání deště Δτ bude stejný pro vstup v jakémkoliv časovém intervalu, nezáleží na čase začátku intervalu. Výsledný odtok v určitém čase je poté dán součtem jednotlivých upravených pořadnic jednotkového hydrogramu u(t).P_ef.

Skládání TUH s využitím principů superpozice a časové invariance

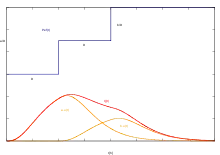
Postupnou transformaci efektivního deště P_ef(t) jednotkovým hydrogramem u(t) na odtok Q(t) popisují genetické rovnice. Jednotlivé hodnoty efektivního deště, pořadnic jednotkového hydrogramu a výsledného odtoku přísluší časovým intervalům délky Δτ:

${\displaystyle Q_{1}=P_{ef\,1}\,u_{1}}$

${\displaystyle Q_{2}=P_{ef\,1}\,u_{2}+P_{ef\,2}\,u_{1}}$

${\displaystyle Q_{3}=P_{ef\,1}\,u_{3}+P_{ef\,2}\,u_{2}+P_{ef\,3}\,u_{1}}$

${\displaystyle \vdots }$

${\displaystyle Q_{m}=P_{ef\,1}\,u_{m}+P_{ef\,2}\,u_{m-1}+\ldots +P_{ef\,m-1}\,u_{2}+P_{ef\,m}\,u_{1}}$

${\displaystyle Q_{m+1}=P_{ef\,1}\,u_{m+1}+\ldots +P_{ef\,2}\,u_{m}+P_{ef\,m}\,u_{2}}$

${\displaystyle \vdots }$

${\displaystyle Q_{m+n-2}=P_{ef\,m-1}\,u_{n}+P_{ef\,m}\,u_{n-1}}$

${\displaystyle Q_{m+n-1}=P_{ef\,m}\,u_{n}}$

Obecně lze tuto konvoluční proceduru zapsat rovnicí

${\displaystyle Q_{i}=\sum _{k=1}^{i}P_{ef\,k}\,u_{i-k+1}}$

Indexy i a k značí pořadí časového intervalu délky Δτ od času počátečního vstupu.

Pro hodnoty P_ef(t), u(t), Q(t) v čase t se rovnice konvoluce upraví na tvar

${\displaystyle Q(t)=\Delta \tau \sum _{k=0}^{t/\Delta \tau }P_{ef}(k\Delta \tau )\,u(t-k\Delta \tau )}$

Odvození S-křivky S(t) pro stálou jednotkovou intenzitu

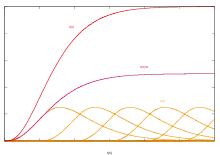
S-křivka vznikne sečtením pořadnic jednotkových hydrogramů pro efektivní déšť doby trvání D, které jsou vzájemně posunuté o čas D. Jedná se tedy o odezvu povodí na efektivní déšť o stálé intenzitě I=1/D a neomezené době trvání.

Vynásobením pořadnic takto získané S-křivky dobou trvání efektivního deště D (čemuž odpovídá dělení intenzitou I) dostaneme S-křivku S(t) pro stálou jednotkovou intenzitu.

Odvození TUH u(t) pro déšť doby trvání D' z jednotkové S-křivky S(t)

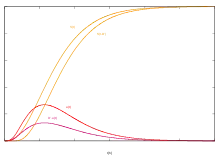
Z ní lze odvodit pořadnice TUH u'(t) pro libovolnou dobu trvání deště D', a to jako rozdíl pořadnic této S-křivky S(t) a stejné S-křivky posunuté o čas D', vynásobený intenzitou I' odvozovaného TUH či dělený dobou jeho trvání D':

${\displaystyle u'(t)=I'[S(t)-S(t-D')]={\frac {S(t)-S(t-D')}{D'}}}$

Okamžikový jednotkový hydrogram (instantaneous unit hydrograph, zkratka IUH) je hydrogram vyvolaný efektivním deštěm o jednotkovém objemu zasahujícím povodí během nekonečně krátké doby (tj. doby D→0), přitom opět platí předpoklad rovnoměrného rozmístění na povodí a principy superpozice a časové invariance. Matematicky se jedná o Greenovu funkci, což je odezva na Diracovu delta funkci (Diracův jednotkový impuls).

Rovnice konvoluce, ve které pravá strana představuje konvoluční integrál, má tvar:

${\displaystyle Q(t)=\int \limits _{0}^{t}u(\tau )\,P_{ef}(t-\tau )\,d\tau }$

Q(t) představuje odtokový výstup, P_ef vstup efektivního deště a u(t) okamžikový jednotkový hydrogram. Výstup se určuje pro daný čas t, τ je pomocná proměnná při konvoluci.

Tato rovnice vznikne z rovnice konvoluce P_ef a TUH po zkrácení časového kroku na limitní případ Δτ→0. Diskretizací spojitého vstupu P_ef na časové intervaly Δτ se dosáhne opačného převodu.

Okamžikový jednotkový hydrogram u(t) lze také interpretovat jako první derivaci S-křivky S(t) vyvolané deštěm jednotkové intenzity:

${\displaystyle u(t)={\frac {\mathrm {d} S(t)}{\mathrm {d} t}}}$

Pořadnice TUH u_TUH(t) pro déšť doby trvání D se dají zjistit jako průměr všech pořadnic IUH z intervalu od t-D do t:

${\displaystyle u_{TUH}(t)={\frac {1}{D}}\int \limits _{t-D}^{t}u_{IUH}(s)\,ds}$

Pro přibližný výpočet lze pro dostatečně malé D použít vztah:

${\displaystyle u_{TUH}(t)={\frac {u_{IUH}(t-D)+u_{IUH}(t)}{2}}}$

Nahrazení přírodních povodí lineárním systémem je pouze přibližné a platnost principů omezená. Podle principu superpozice je odezva lineárně závislá na vstupu, což bývá splněno pouze při běžných srážkových vstupech. Při extrémně vysokých dochází k vyššímu kulminačnímu průtoku a kratší kulminační době, nebo naopak v případě vybřežení vodního toku k nižšímu kulminačnímu průtoku a delší kulminační době.

Princip časové invariance předpokládá neměnný stav povodí a jeho charakteristik, ve skutečnosti se však vlastnosti povodí, které ovlivňují odtok, mění (například nasycenost půdy závisí na úhrnu srážek v předchozí době).

Kvůli předpokladu rovnoměrného rozložení srážky na povodí je vhodné metodu jednotkového hydrogramu používat jen na povodí do určité rozlohy.

Pro určení jednotkového hydrogramu z měřených dat je třeba nejdříve zjistit efektivní déšť z měřených srážek a separovat základní odtok z měřených odtoků, nejlépe tak, aby byl objem efektivního deště roven objemu přímého odtoku.

Pokud se na povodí vyskytl jednoduchý efektivní déšť požadované doby trvání D, stačí pro určení jednotkového hydrogramu vydělit hodnoty přímého odtoku příslušnou intenzitou efektivního deště. Z různých efektivních dešťů o stejné době trvání budou odvozeny různé jednotkové hydrogramy, pořadnice výsledného TUH pro efektivní déšť doby trvání D se určí jako aritmetický průměr pořadnic jednotlivých různých TUH.

Obvykle má však efektivní déšť intenzitu proměnlivou. Pořadnice jednotkového hydrogramu u(t) (pro efektivní déšť doby trvání rovnající se časovému kroku dat) se získají řešením soustavy genetických rovnic. Tato soustava m+n-1 rovnic má n neznámých, pořadnice jednotkového hydrogramu umožňuje určit metoda nejmenších čtverců (lineární regrese mezi efektivním deštěm a přímými odtoky), metoda momentů a další metody.

Jednotkový hydrogram lze matematicky popsat některou z vhodných funkcí charakterizovanou parametry. Pro určení jednotkového hydrogramu poté stačí znalost několika parametrů, což umožňuje snazší kalibraci modelu a také zjednodušuje odvozování jednotkových hydrogramů pro povodí, kde nejsou k dispozici měřená data.

Existují empirické křivky, jejichž parametry lze zjistit z charakteristik povodí, bývají však často omezeny na oblasti, pro které byly odvozeny. Jednou z nich je Snyderův jednotkový hydrogram. Jeho tvar se určuje pomocí času kulminace, doby trvání hydrogramu, kulminačního průtoku a doby mezi výskytem průtoků o velikosti 50 % a 75 % z kulminačního průtoku na vzestupné a sestupné větvi. Tyto údaje se zjišťují z geografických vlastností a koeficientů charakterizujících danou lokalitu.

Na podobných principech jsou založeny například jednotkový hydrogram US SCS a Espeyův jednotkový hydrogram.

Lze použít také jednotkové hydrogramy představující odezvu na jednotkový vstup do soustavy prvků s transformační funkcí (lineárních kanálů a lineárních nádrží). Takové soustavy do určité míry napodobují skutečné procesy v povodí. Například výstupem z jednoduché série lineárních nádrží (zvané také Nashova kaskáda či Nashův model) je jednotkový hydrogram odpovídající gamma rozdělení.

Jako jednotkový hydrogram je možno chápat rozdělení dob doběhu na ploše povodí, které se označuje jako křivka time-area. Pořadnicím jednotkového hydrogramu odpovídá velikost izochron, částí plochy povodí se stejnou dobou doběhu do uzavírajícího profilu.

Clarkův jednotkový hydrogram je výstup získaný metodou time-area, který je dále transformován lineární nádrží.

• Wilfried Brutsaert: Hydrology. Cambridge University Press, New York, 2005.
• Warren Viessman, Garry Lewis: Introduction to hydrology. Prentice Hall, 2002.