Rozdělení gama

Rozdělení gama je v teorii pravděpodobnosti a statistiky dvouparametrická rodina spojitých rozdělení pravděpodobnosti. Speciálními případy distribuce gama jsou exponenciální rozdělení, Erlangovo rozdělení a rozdělení chí-kvadrát. Běžně se používají tři různé parametrizace distribuce gama:

1. S parametrem tvaru k a parametrem měřítka θ.
2. S parametrem tvaru α = k a inverzním parametrem měřítka β = 1/θ.
3. S tvarovým parametrem k a střední hodnotou μ = kθ = α/β.

Grafy hustot gama rozdělení s různými charakteristikami.

Grafy distribučních funkcí rozdělení gama s různými charakteristikami.

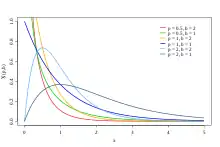
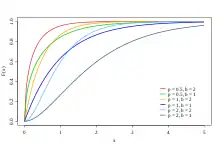
V každé z těchto tří forem jsou oba parametry kladná reálná čísla.

Distribuci gama lze parametrizovat například pomocí tvarového parametru α = k a inverzního parametru škály β = 1 / θ. Mějme náhodnou proměnnou X, která má rozdělení gama s parametry α a β:

${\displaystyle X\sim \Gamma (\alpha ,\beta )\equiv \operatorname {Gama} (\alpha ,\beta )}$.

Odpovídající funkce hustoty pravděpodobnosti v této parametrizaci je

${\displaystyle {\begin{aligned}f(x;\alpha ,\beta )&={\frac {\beta ^{\alpha }x^{\alpha -1}e^{-\beta x}}{\Gamma (\alpha )}}\quad {\text{ pro }}x>0\quad \alpha ,\beta >0,\\[6pt]\end{aligned}}}$

kde ${\displaystyle \Gamma (\alpha )}$ je funkce gama . Pro všechna kladná celá čísla ${\displaystyle \Gamma (\alpha )=(\alpha -1)!}$ .

Kumulativní distribuční funkce je regularizovaná funkce gama:

${\displaystyle F(x;\alpha ,\beta )=\int _{0}^{x}f(u;\alpha ,\beta )\,du={\frac {\gamma (\alpha ,\beta x)}{\Gamma (\alpha )}},}$

kde ${\displaystyle \gamma (\alpha ,\beta x)}$ je nižší neúplná funkce gama.

Pokud α je kladné celé číslo (tj. distribuce je Erlangovo rozdělení), má tato distribuční funkce následující rozvoj do řady:[1]

${\displaystyle F(x;\alpha ,\beta )=1-\sum _{i=0}^{\alpha -1}{\frac {(\beta x)^{i}}{i!}}e^{-\beta x}=e^{-\beta x}\sum _{i=\alpha }^{\infty }{\frac {(\beta x)^{i}}{i!}}.}$

${\displaystyle f(x;k,\theta )={\frac {x^{k-1}e^{-{\frac {x}{\theta }}}}{\theta ^{k}\Gamma (k)}}\quad {\text{ pro }}x>0{\text{ a }}k,\theta >0.}$