Izochorický děj

V případě ideálního plynu lze pro izochorický děj ze stavové rovnice odvodit Charlesův zákon

${\displaystyle {\frac {p}{T}}={\mbox{konst}}}$,

kde ${\displaystyle p}$ je tlak a ${\displaystyle T}$ je termodynamická teplota plynu. Při izochorickém ději je tedy podíl tlaku a termodynamické teploty ideálního plynu stálý.

Izochora.

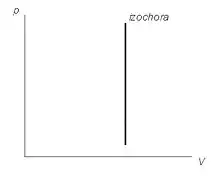
Závislost tlaku na objemu při izochorickém ději je v p-V diagramu vyjádřena přímkou rovnoběžnou s osou p, která se nazývá izochora.

Pro termodynamické systémy schopné konat pouze objemovou práci (nebo u kterých je konání jiných druhů práce zanedbatelné) platí:

Poněvadž se při izochorickém ději nemění objem ${\displaystyle V}$, bude podle první věty termodynamické platit vztah

${\displaystyle \delta Q=\mathrm {d} U}$,

kde ${\displaystyle Q}$ je teplo a ${\displaystyle U}$ je vnitřní energie.

Protože ${\displaystyle \delta A=p\mathrm {d} V}$ je objemová práce vykonaná plynem (nebo dodaná plynu), lze tvrdit, že ${\displaystyle \delta A=0}$. To znamená, že při izochorickém ději plyn nevykonává (ani nepřijímá) žádnou práci.

Při izochorickém ději je všechno dodané (nebo odevzdané) teplo použito na zvýšení (nebo snížení) vnitřní energie ${\displaystyle U}$.

Teplo dodané plynu zvýší jeho teplotu o ${\displaystyle \Delta T}$. K vyjádření tohoto tepla lze použít molární tepelnou kapacitu při stálém objemu ${\displaystyle C_{V}}$, tedy

${\displaystyle \delta Q=nC_{V}\mathrm {d} T=\mathrm {d} U}$,

kde ${\displaystyle n}$ je látkové množství. Integrací tohoto vztahu dostaneme

${\displaystyle Q=nC_{V}(T_{2}-T_{1})=\Delta U}$

Vztah pro entropii při vratném izochorickém ději lze vyjádřit pomocí předchozích vztahů ve tvaru

${\displaystyle \Delta S=nC_{V}\ln {\frac {T_{2}}{T_{1}}}=nC_{V}\ln {\frac {p_{2}}{p_{1}}}}$

Dodáme-li soustavě při vratném izobarickém ději stejné množství tepla jako při vratném ději izochorickém, bude přírůstek teploty plynu při izobarickém ději menší než při izochorickém ději. Pro molární tepelné kapacity tedy platí ${\displaystyle C_{p}>C_{V}}$.

Vztah mezi ${\displaystyle C_{p}}$ a ${\displaystyle C_{V}}$ určuje Poissonova konstanta a Mayerův vztah.

• Termodynamický děj
• Charlesův zákon
• Termodynamika

• Obrázky, zvuky či videa k tématu Izochorický děj na Wikimedia Commons